Question

When proving that a quadrilateral is a parallelogram by using slopes you must find
A. The slopes of all four sides
B. The slope of two opposite sides
C. The lengths of all four sides
D. Both the lengths and slopes of all four sides
E. None of These

Answer 1

Hint: To solve the problem, we are going to take the four points in the coordinate system which forms a closed shape in two dimensional. Now we will find the all the lengths of the sides of the shape using the formula distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ i.e. $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$. Then we will calculate the angles of the shape by using the slopes of the sides. We know the formula for the slope of the line formed by the points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. Now we will check that the quadrilateral is a parallelogram or not by using the values of length of sides and slopes.

Complete step by step answer:
Let us consider $4$points in a two-dimensional coordinate system. They are $A\left( -4,-3 \right),B\left( 3,1 \right),C\left( 3,6 \right),D\left( -4,2 \right)$ as shown in below figure

Now finding the lengths of the sides by using the distance between two points formula i.e. $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Length of $AB$is
$\begin{align}
  & AB=\sqrt{{{\left( 3+4 \right)}^{2}}+\left( 1+3 \right)} \\
 & =\sqrt{{{7}^{2}}+{{4}^{2}}} \\
 & =\sqrt{49+16} \\
 & =\sqrt{65} \\
 & \simeq 8.1
\end{align}$
Length of $BC$ is
$\begin{align}
  & BC=\sqrt{{{\left( 3-3 \right)}^{2}}+{{\left( 6-1 \right)}^{2}}} \\
 & =\sqrt{{{5}^{2}}} \\
 & =5
\end{align}$
Length of $CD$ is
$\begin{align}
  & CD=\sqrt{{{\left( -4-3 \right)}^{2}}+{{\left( 2-6 \right)}^{2}}} \\
 & =\sqrt{{{\left( -7 \right)}^{2}}+{{\left( -4 \right)}^{2}}} \\
 & =\sqrt{49+16} \\
 & =\sqrt{65} \\
 & \simeq 8.1
\end{align}$
Length of $DA$ is
$\begin{align}
  & DA=\sqrt{{{\left( -4+4 \right)}^{2}}+{{\left( -3-2 \right)}^{2}}} \\
 & =\sqrt{{{\left( -5 \right)}^{2}}} \\
 & =5
\end{align}$
Here we get
$\begin{align}
  & AB=8.1 \\
 & BC=5 \\
 & CD=8.1 \\
 & DA=5 \\
\end{align}$
i.e. the lengths of opposite sides of the quadrilateral are equal. But we can’t say this quadrilateral is parallelogram without finding the angle of the quadrilateral. Finding the angles between the lines takes a lot of calculation and time. So for that we will find the slopes of all the lines and if we get the slopes of opposite sides are same then the angle between them are also same. Hence we conclude the problem.
Slope of line $AB$is
$\begin{align}
  & {{m}_{1}}=\dfrac{1+3}{3+4} \\
 & =\dfrac{4}{7}
\end{align}$
Slope of line $BC$is
$\begin{align}
  & {{m}_{2}}=\dfrac{6-1}{3-3} \\
 & =\propto
\end{align}$
Slope of line $CD$ is
$\begin{align}
  & {{m}_{3}}=\dfrac{6-2}{3+4} \\
 & =\dfrac{4}{7}
\end{align}$
Slope of line $DA$ is
$\begin{align}
  & {{m}_{4}}=\dfrac{2+3}{-4+4} \\
 & =\propto
\end{align}$
Here we get the slopes of opposite sides are equal then the angle between the lines are also the same. Hence the shape formed by the coordinates is Parallelogram.

So, the correct answer is “Option D”.

Note: Quadrilateral: In geometry quadrilateral is defined as a closed, two-dimensional shape which has four sides. The quadrilateral has four vertices/corners. The distance between the adjacent corners/vertices is called the length of the side formed by those vertices/corners.
Parallelogram: Parallelogram is defined as the Quadrilateral in which the opposite sides have equal length and opposite angles are equal. In geometry all the squares. Rectangles and Rhombuses are coming under the section of parallelogram.

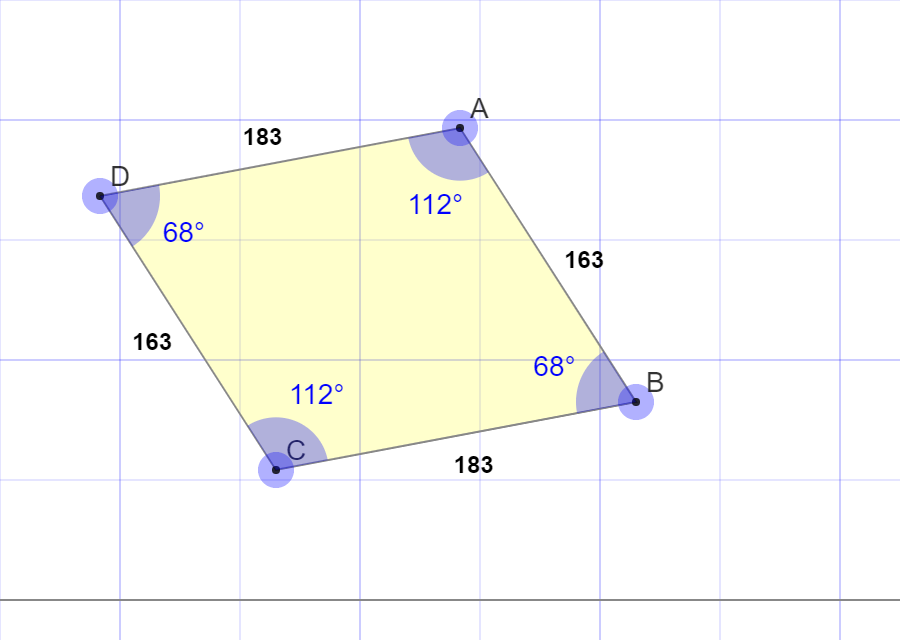
In the above figure we can say the following statements
1. The figure is closed and a two-dimensional shape having four sides. Hence the shape is called a quadrilateral.
2. In figure the lengths of opposite sides and the opposite angles are the same. Hence the quadrilateral is a parallelogram.