Question

Prove the law of conservation of energy for a particle performing simple harmonic motion. Hence graphically show the variation of kinetic energy and potential energy w.r.t. instantaneous displacement.

Answer 1

Hint: Calculate the total energy i.e. the sum of kinetic and potential energies of the particle in SHM at different values of displacement i.e. (i) when displacement is at any variable distance x, (ii) when displacement x=A (maximum displacement/amplitude) and (iii) when displacement x=0 (mean position)
The total energy of the particle will always remain constant.

Formula Used: he kinetic energy and potential energy of a particle performing SHM is given by:

K.E = $\dfrac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right)$
P.E = $\dfrac{1}{2}m{\omega ^2}{x^2}$

Complete step by step answer:
Consider a particle of mass m, performing linear simple harmonic motion.
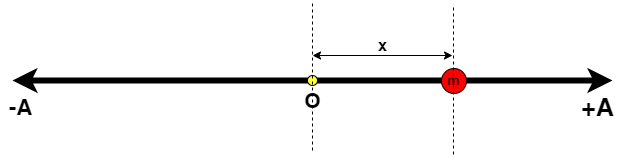
We take three cases when displacement of the particle, x varies.

Case1: Particle is at displacement x from the mean position O.
Here kinetic energy of the particle is:
 $KE = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
Potential Energy of particle at x:
$PE = \dfrac{1}{2}m{\omega ^2}{x^2}$
Hence, Total energy = KE+PE
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2}) + \dfrac{1}{2}m{\omega ^2}{x^2}$
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2} + {x^2})$
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}{A^2}$ ………eq1
Case2: Particle is at mean position i.e. x=0

Here, kinetic energy of particle is:
$KE = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}({A^2} - {0^2}) = \dfrac{1}{2}m{\omega ^2}{A^2}$
Potential energy at x=0 is:
$PE = \dfrac{1}{2}m{\omega ^2}{x^2}$
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}{0^2} \Rightarrow 0$
Hence, total energy=KE+PE
 $ \Rightarrow \dfrac{1}{2}m{\omega ^2}{A^2} + 0$
$ \Rightarrow \dfrac{1}{2}m{\omega ^2}{A^2}$ ……………eq2
Case3: Particle at maximum displacement from mean position i.e. x=A (A=Amplitude of SHM)

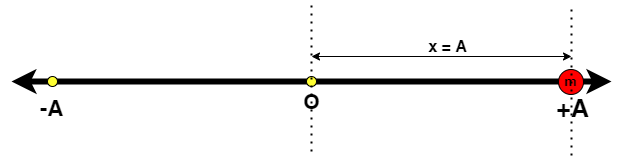
Here, kinetic energy of particle is:
$KE = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$ $ \Rightarrow \dfrac{1}{2}m{\omega ^2}({A^2} - {A^2}) \Rightarrow 0$
Potential energy of particle is:
$PE = \dfrac{1}{2}m{\omega ^2}{x^2}$ $ \Rightarrow \dfrac{1}{2}m{\omega ^2}{A^2}$
Hence, total energy=KE+PE
 $ \Rightarrow 0 + \dfrac{1}{2}m{\omega ^2}{A^2}$ $ \Rightarrow \dfrac{1}{2}m{\omega ^2}{A^2}$ ……………eq3
From equations 1, 2 and 3, we can observe that the total energy of the particle performing linear simple harmonic motion at any point in its path, remains constant.
Hence Proved.
Variation of kinetic energy and potential energy w.r.t. instantaneous displacement is:

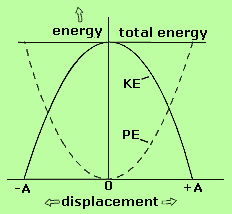
Note:The kinetic energy and potential energy of the particle in SHM can also be given in the terms of phase angle.
So, considering the particle to be at mean position at time t = 0, the equations for its displacement will be given by:
$x = A\sin \omega t$
So, we get:
K.E = $\dfrac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\omega t$
P.E = $\dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\omega t$
Adding them the total energy will again come out to be constant.