Question

How do I prove the identity $\tan \theta \sin \theta + \cos \theta \equiv \sec \theta $?

Answer 1

Hint: First, take the left side of identity. Write $\tan \theta $ in sines and cosines using the quotient identity and simplify it. Next, apply Pythagorean identity in reverse and Combine the numerators over the common denominator. We will get the right side of identity.

Formula used:
$\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$
${\sin ^2}\theta + {\cos ^2} = 1$
$\cos \theta = \dfrac{1}{{\sec \theta }}$

Complete step by step answer:
To prove: $\tan \theta \sin \theta + \cos \theta \equiv \sec \theta $
We will start on the left side.
${\text{LHS}} = \tan \theta \sin \theta + \cos \theta $
Write $\tan \theta $ in sines and cosines using the quotient identity.
$ \Rightarrow {\text{LHS}} = \dfrac{{\sin \theta }}{{\cos \theta }}\sin \theta + \cos \theta $
Write $\sin \theta $ as a fraction with denominator $1$.
$ \Rightarrow {\text{LHS}} = \dfrac{{\sin \theta }}{{\cos \theta }} \cdot \dfrac{{\sin \theta }}{1} + \cos \theta $
Combine.
$ \Rightarrow {\text{LHS}} = \dfrac{{\sin \theta \cdot \sin \theta }}{{\cos \theta \times 1}} + \cos \theta $
Multiply $\sin \theta \times \sin \theta $.
$ \Rightarrow {\text{LHS}} = \dfrac{{{{\sin }^2}\theta }}{{\cos \theta \times 1}} + \cos \theta $
Multiply $\cos \theta $ by $1$.
$ \Rightarrow {\text{LHS}} = \dfrac{{{{\sin }^2}\theta }}{{\cos \theta }} + \cos \theta $
Apply Pythagorean identity in reverse.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta }}{{\cos \theta }} + \cos \theta $
To write $\dfrac{{\cos \theta }}{1}$ as a fraction with a common denominator, multiply by $\dfrac{{\cos \theta }}{{\cos \theta }}$.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta }}{{\cos \theta }} + \dfrac{{\cos \theta }}{{\cos \theta }} \cdot \dfrac{{\cos \theta }}{{\cos \theta }}$
Write each expression with a common denominator of $\cos \theta $, by multiplying each by an appropriate factor of $1$.
Combine.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta }}{{\cos \theta }} + \dfrac{{\cos \theta \times \cos \theta }}{{\cos \theta \times 1}}$
Multiply $\cos \theta $ by $1$.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta }}{{\cos \theta }} + \dfrac{{\cos \theta \times \cos \theta }}{{\cos \theta }}$
Multiply $\cos \theta \times \cos \theta $.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta }}{{\cos \theta }} + \dfrac{{{{\cos }^2}\theta }}{{\cos \theta }}$
Combine the numerators over the common denominator.
$ \Rightarrow {\text{LHS}} = \dfrac{{1 - {{\cos }^2}\theta + {{\cos }^2}\theta }}{{\cos \theta }}$
Simplify the numerator.
$ \Rightarrow {\text{LHS}} = \dfrac{1}{{\cos \theta }}$
Rewrite $\dfrac{1}{{\cos \theta }}$ as $\sec \theta $.
$ \Rightarrow {\text{LHS}} = \sec \theta $
$\therefore {\text{LHS}} = {\text{RHS}}$
Because the two sides have been shown to be equivalent, the equation is an identity.
$\tan \theta \sin \theta + \cos \theta \equiv \sec \theta $ is an identity
Final solution: Hence, $\tan \theta \sin \theta + \cos \theta \equiv \sec \theta $.

Additional information:
Trigonometric identity: An equation involving trigonometric ratios of an angle $\theta $ (say) is said to be a trigonometric identity if it is satisfied for all values of $\theta $ for which the given trigonometric ratios are defined.
For example, ${\cos ^2}\theta - \dfrac{1}{2}\cos \theta = \cos \theta \left( {\cos \theta - \dfrac{1}{2}} \right)$ is a trigonometric identity, whereas $\cos \theta \left( {\cos \theta - \dfrac{1}{2}} \right) = 0$ is an equation.
Also, $\sec \theta = \dfrac{1}{{\cos \theta }}$ is a trigonometric identity, because it holds for all values of $\theta $ except for which $\cos \theta = 0$. For $\cos \theta = 0$, $\sec \theta $ is not defined.

Note: In above question, we can prove the identity by plotting the left side and the right side of the identity separately.
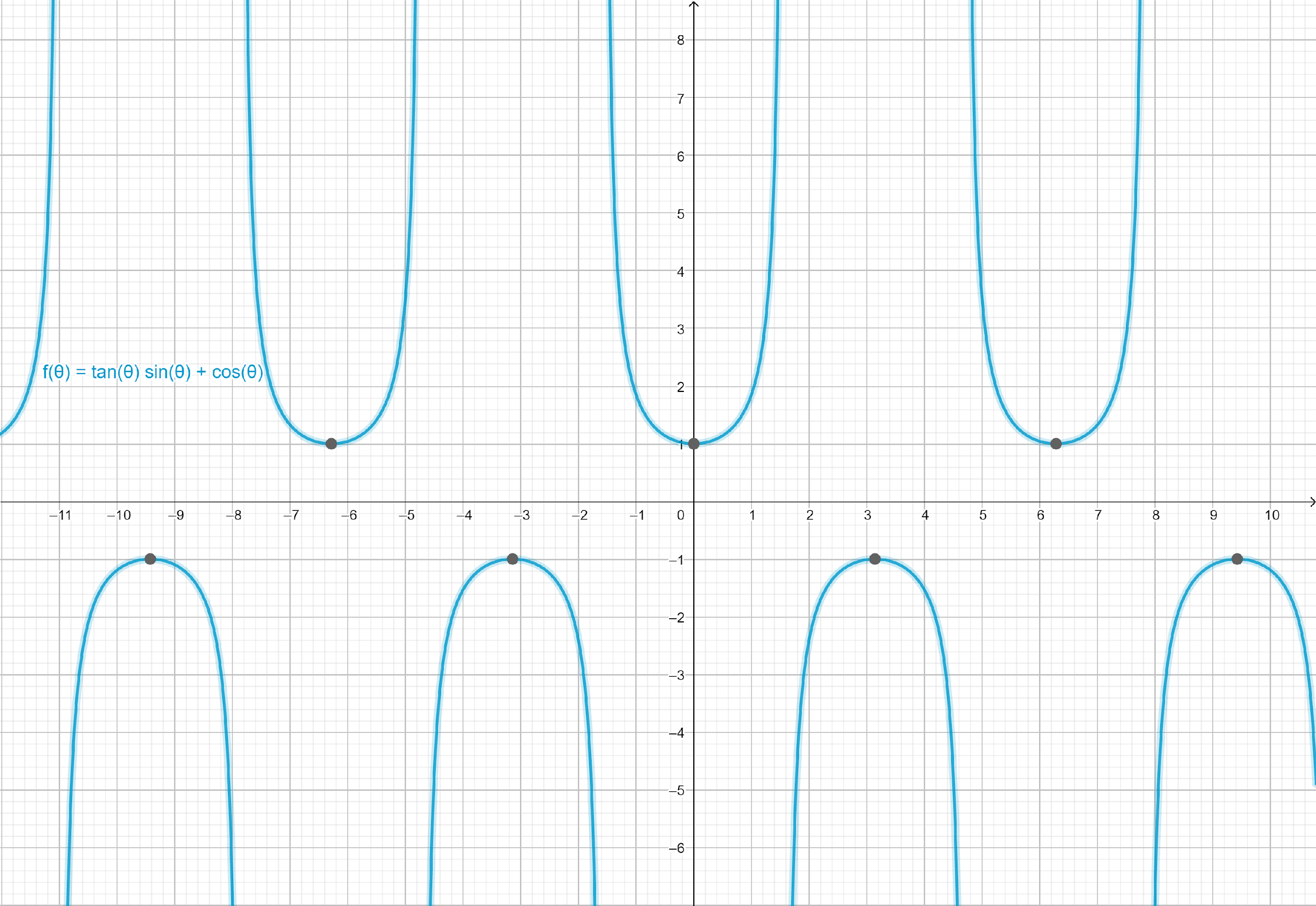
Graph of $f\left( \theta \right) = \tan \theta \sin \theta + \cos \theta $:

Graph of $g\left( \theta \right) = \sec \theta $:

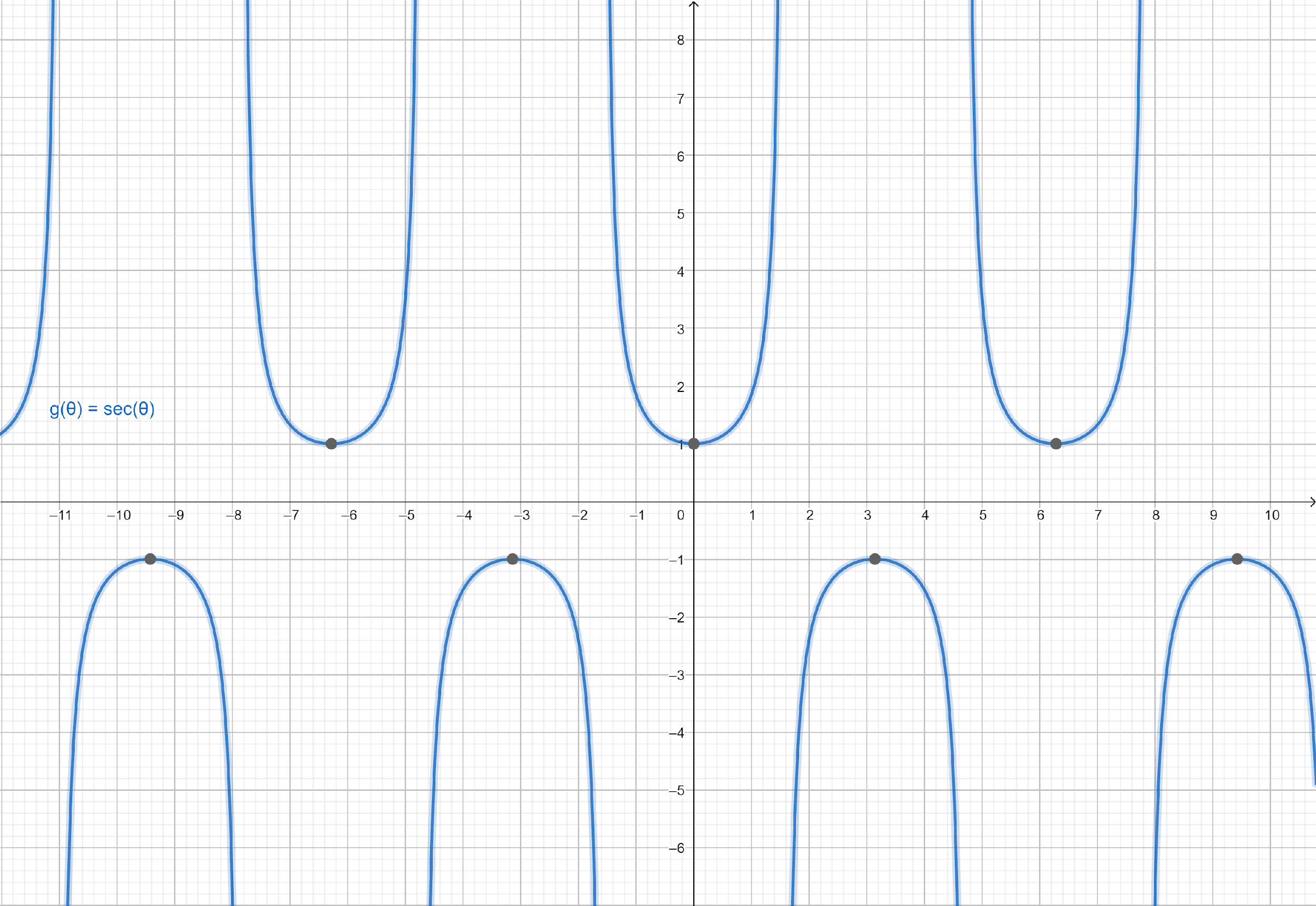
Both functions have the same graph, meaning they are equal or coincide at every point.
Final solution: Hence, $\tan \theta \sin \theta + \cos \theta \equiv \sec \theta $.