
Prove the given inverse trigonometric expression ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)={{\sin }^{-1}}\left( \dfrac{5}{13} \right)+{{\cos }^{-1}}\left( \dfrac{3}{5} \right)$.
Answer
583.8k+ views
Hint:We start solving this problem by first bringing ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$ to the LHS and convert the given sine inverse functions, in the L.H.S, into cosine inverse functions. In the given two sine inverse functions, we assume the numerator as perpendicular and denominator as hypotenuse. Then we find the base in both the terms using Pythagoras theorem given by $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$. Then after converting them into cosine inverse, we use the formula ${{\cos }^{-1}}x-{{\cos }^{-1}}y={{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$, if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$, and check if the values we got satisfy the assumed formula and find the value of it, thereby proving the given statement.
Complete step-by-step solution:
First let us change ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)$ into cosine inverse function.
Let us assume that ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)=\alpha $. Now let us find the value of $\cos \alpha $.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$, therefore, $\theta ={{\sin }^{-1}}\left( \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \right)$. On comparing we get that, in ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)$, 63 is the perpendicular and 65 is the hypotenuse.
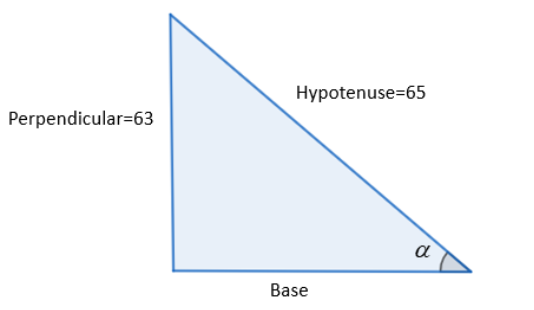
Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{align}
& \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
& \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{{{65}^{\text{2}}}-{{63}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{\left( 65+63 \right)\left( 65-63 \right)} \\
& \Rightarrow \text{base}=\sqrt{2\times 128} \\
& \Rightarrow \text{base}=\sqrt{256} \\
& \Rightarrow \text{base}=16 \\
\end{align}$
Now, we know that, $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$.
So, we get the value $\cos \alpha =\dfrac{16}{65}$. Then we get,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{63}{65} \right)=\alpha ={{\cos }^{-1}}\left( \dfrac{16}{65} \right).............\left( 1 \right)$
Similarly, let us change ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$ into cosine inverse function.
Let us assume that ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)=\beta $. Now let us find the value of $\cos \beta $.
In ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$, 5 is the perpendicular and 13 is the hypotenuse.
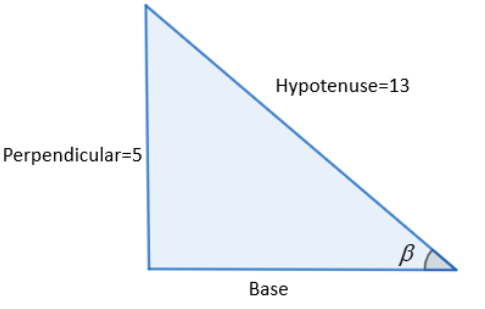
Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{align}
& \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
& \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{{{13}^{\text{2}}}-{{5}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{169-25} \\
& \Rightarrow \text{base}=\sqrt{144}=12 \\
\end{align}$
So, we get the value $\cos \beta =\dfrac{12}{13}$. Then we get,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{5}{13} \right)=\beta ={{\cos }^{-1}}\left( \dfrac{12}{13} \right).........\left( 2 \right)$
From equations (1) and (2) we can say that,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{63}{65} \right)-{{\sin }^{-1}}\left( \dfrac{5}{13} \right)={{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)..........\left( 3 \right)$
Now let us consider the value ${{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)$.
Now let us consider the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y={{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$.
Now let us verify if we can apply this formula or not.
Here $x=\dfrac{16}{65}\text{ and }y=\dfrac{12}{13}$ are greater than zero.
$\begin{align}
& \Rightarrow {{\left( \dfrac{16}{65} \right)}^{2}}+{{\left( \dfrac{12}{13} \right)}^{2}} \\
& \Rightarrow \dfrac{256}{4225}+\dfrac{144}{169} \\
& \Rightarrow \dfrac{256+3600}{4225} \\
& \Rightarrow \dfrac{3856}{4225}\le 1 \\
\end{align}$
So, we can use the above formula. Then we get,
\[\begin{align}
& {{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{16}{65}\times \dfrac{12}{13}+\sqrt{1-{{\left( \dfrac{16}{65} \right)}^{2}}}\sqrt{1-{{\left( \dfrac{12}{13} \right)}^{2}}} \right) \\
\end{align}\]
Squaring the values that are inside the square roots, we get,
\[\begin{align}
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{1-\dfrac{256}{4225}}\sqrt{1-\dfrac{144}{169}} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{\dfrac{3969}{4225}}\sqrt{\dfrac{25}{169}} \right) \\
\end{align}\]
Now let us write them as the squares,
\[={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{{{\left( \dfrac{63}{65} \right)}^{2}}}\sqrt{{{\left( \dfrac{5}{13} \right)}^{2}}} \right)\]
Finding the square roots in the above expression, we get,
\[={{\cos }^{-1}}\left( \dfrac{192}{845}+\dfrac{63}{65}\times \dfrac{5}{13} \right)\]
\[\begin{align}
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\dfrac{315}{845} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{192+315}{845} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{507}{845} \right) \\
\end{align}\]
Simplifying it we get,
\[={{\cos }^{-1}}\left( \dfrac{3}{5} \right)\]
So, we get that ${{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)={{\cos }^{-1}}\dfrac{3}{5}$.
Substituting this value in equation (3) we get,
${{\sin }^{-1}}\left( \dfrac{63}{65} \right)-{{\sin }^{-1}}\left( \dfrac{5}{13} \right)={{\cos }^{-1}}\left( \dfrac{3}{5} \right)$
Now, taking ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$ to the R.H.S, we get,
${{\sin }^{-1}}\left( \dfrac{63}{65} \right)={{\sin }^{-1}}\left( \dfrac{5}{13} \right)+{{\cos }^{-1}}\left( \dfrac{3}{5} \right)$
Hence Proved.
Note: There is a possibility of one making a mistake while solving this problem by not checking the if the values we have for x and y satisfy the conditions for the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y={{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$. Then, if they satisfy these conditions, we will use this formula otherwise we need to use the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y=\pi -{{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\ge 1$.
Complete step-by-step solution:
First let us change ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)$ into cosine inverse function.
Let us assume that ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)=\alpha $. Now let us find the value of $\cos \alpha $.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$, therefore, $\theta ={{\sin }^{-1}}\left( \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \right)$. On comparing we get that, in ${{\sin }^{-1}}\left( \dfrac{63}{65} \right)$, 63 is the perpendicular and 65 is the hypotenuse.

Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{align}
& \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
& \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{{{65}^{\text{2}}}-{{63}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{\left( 65+63 \right)\left( 65-63 \right)} \\
& \Rightarrow \text{base}=\sqrt{2\times 128} \\
& \Rightarrow \text{base}=\sqrt{256} \\
& \Rightarrow \text{base}=16 \\
\end{align}$
Now, we know that, $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$.
So, we get the value $\cos \alpha =\dfrac{16}{65}$. Then we get,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{63}{65} \right)=\alpha ={{\cos }^{-1}}\left( \dfrac{16}{65} \right).............\left( 1 \right)$
Similarly, let us change ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$ into cosine inverse function.
Let us assume that ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)=\beta $. Now let us find the value of $\cos \beta $.
In ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$, 5 is the perpendicular and 13 is the hypotenuse.

Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{align}
& \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
& \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{{{13}^{\text{2}}}-{{5}^{\text{2}}}} \\
& \Rightarrow \text{base}=\sqrt{169-25} \\
& \Rightarrow \text{base}=\sqrt{144}=12 \\
\end{align}$
So, we get the value $\cos \beta =\dfrac{12}{13}$. Then we get,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{5}{13} \right)=\beta ={{\cos }^{-1}}\left( \dfrac{12}{13} \right).........\left( 2 \right)$
From equations (1) and (2) we can say that,
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{63}{65} \right)-{{\sin }^{-1}}\left( \dfrac{5}{13} \right)={{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)..........\left( 3 \right)$
Now let us consider the value ${{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)$.
Now let us consider the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y={{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$.
Now let us verify if we can apply this formula or not.
Here $x=\dfrac{16}{65}\text{ and }y=\dfrac{12}{13}$ are greater than zero.
$\begin{align}
& \Rightarrow {{\left( \dfrac{16}{65} \right)}^{2}}+{{\left( \dfrac{12}{13} \right)}^{2}} \\
& \Rightarrow \dfrac{256}{4225}+\dfrac{144}{169} \\
& \Rightarrow \dfrac{256+3600}{4225} \\
& \Rightarrow \dfrac{3856}{4225}\le 1 \\
\end{align}$
So, we can use the above formula. Then we get,
\[\begin{align}
& {{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{16}{65}\times \dfrac{12}{13}+\sqrt{1-{{\left( \dfrac{16}{65} \right)}^{2}}}\sqrt{1-{{\left( \dfrac{12}{13} \right)}^{2}}} \right) \\
\end{align}\]
Squaring the values that are inside the square roots, we get,
\[\begin{align}
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{1-\dfrac{256}{4225}}\sqrt{1-\dfrac{144}{169}} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{\dfrac{3969}{4225}}\sqrt{\dfrac{25}{169}} \right) \\
\end{align}\]
Now let us write them as the squares,
\[={{\cos }^{-1}}\left( \dfrac{192}{845}+\sqrt{{{\left( \dfrac{63}{65} \right)}^{2}}}\sqrt{{{\left( \dfrac{5}{13} \right)}^{2}}} \right)\]
Finding the square roots in the above expression, we get,
\[={{\cos }^{-1}}\left( \dfrac{192}{845}+\dfrac{63}{65}\times \dfrac{5}{13} \right)\]
\[\begin{align}
& ={{\cos }^{-1}}\left( \dfrac{192}{845}+\dfrac{315}{845} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{192+315}{845} \right) \\
& ={{\cos }^{-1}}\left( \dfrac{507}{845} \right) \\
\end{align}\]
Simplifying it we get,
\[={{\cos }^{-1}}\left( \dfrac{3}{5} \right)\]
So, we get that ${{\cos }^{-1}}\left( \dfrac{16}{65} \right)-{{\cos }^{-1}}\left( \dfrac{12}{13} \right)={{\cos }^{-1}}\dfrac{3}{5}$.
Substituting this value in equation (3) we get,
${{\sin }^{-1}}\left( \dfrac{63}{65} \right)-{{\sin }^{-1}}\left( \dfrac{5}{13} \right)={{\cos }^{-1}}\left( \dfrac{3}{5} \right)$
Now, taking ${{\sin }^{-1}}\left( \dfrac{5}{13} \right)$ to the R.H.S, we get,
${{\sin }^{-1}}\left( \dfrac{63}{65} \right)={{\sin }^{-1}}\left( \dfrac{5}{13} \right)+{{\cos }^{-1}}\left( \dfrac{3}{5} \right)$
Hence Proved.
Note: There is a possibility of one making a mistake while solving this problem by not checking the if the values we have for x and y satisfy the conditions for the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y={{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$. Then, if they satisfy these conditions, we will use this formula otherwise we need to use the formula, ${{\cos }^{-1}}x-{{\cos }^{-1}}y=\pi -{{\cos }^{-1}}\left( xy+\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right)$ if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\ge 1$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




