Question

Prove the following statement: $\cos \left( \theta -\phi \right)=\cos \theta \cos \phi +\sin \theta \sin \phi $

Answer 1

Hint: First we are going to draw a diagram and then from that we will try to understand the proof, we are going to use that diagram to draw triangles and with that we will prove the above identity.

We are going to prove $\cos \left( \theta +\phi \right)=\cos \theta \cos \phi -\sin \theta \sin \phi $, and then we will put $-\phi $ in place of $\phi $ , to get the desired answer.

Complete step-by-step answer:

Let’s first look at the diagram,

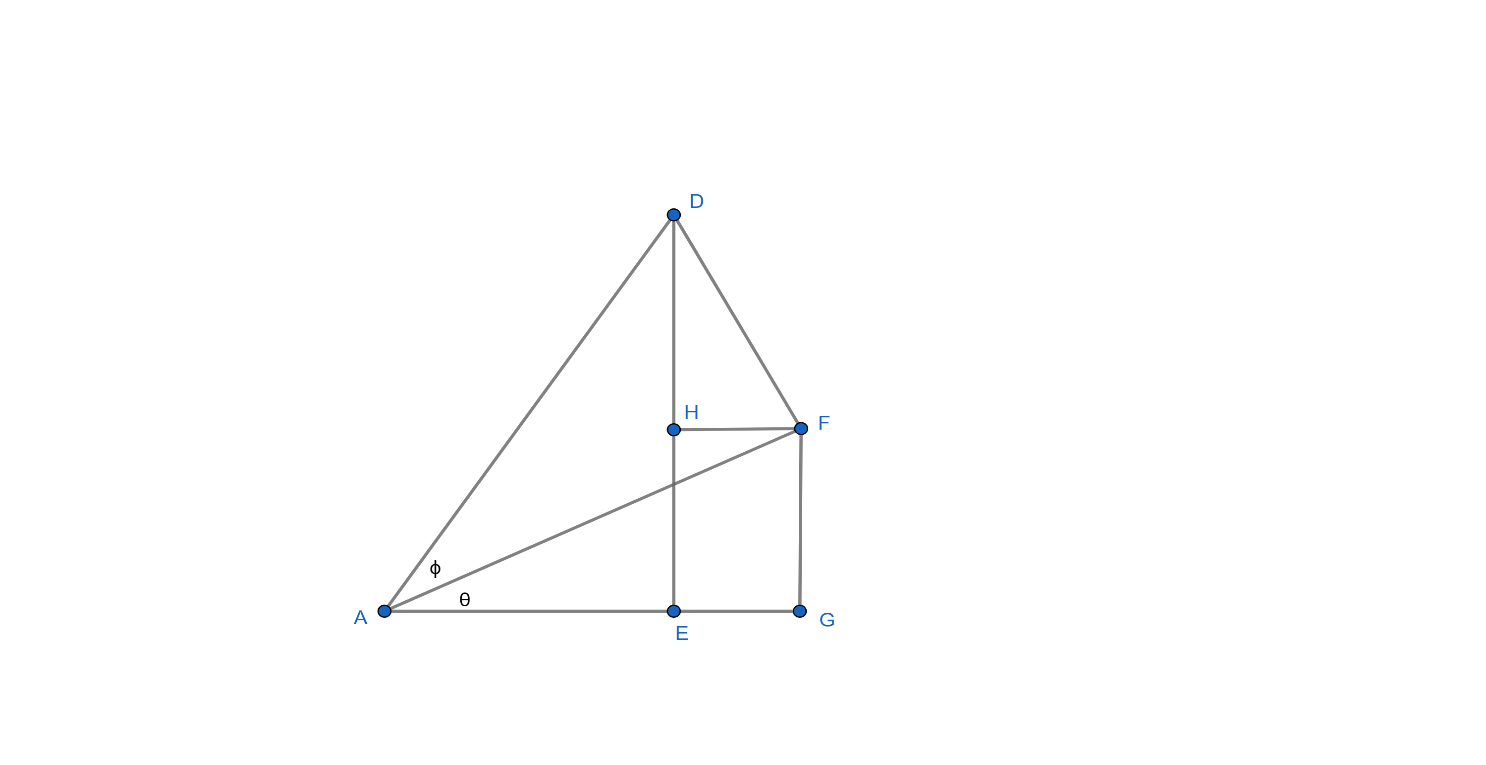
From this diagram we can conclude that,

DF $\bot $ AF

FG $\bot $ AG

HF = EG and HF $\parallel $ EG

These two are alternate angles and hence,

$\angle HFA=\angle FAG$

$\begin{align}

  & \angle DFA=90 \\

 & \angle DFH+\angle HFA=90 \\

 & \angle DFH+\theta =90 \\

 & \angle DFH=90-\theta \\

\end{align}$

Now we know that $\angle DHF=90$ ,

So in $\Delta DHF$ we get,

$\begin{align}

  & \angle HDF=180-\left( 90-\theta \right)-90 \\

 & \angle HDF=\theta \\

\end{align}$

In the given triangle,

$\begin{align}

  & \Delta AED \\

 & \cos \left( \theta +\phi \right)=\dfrac{Base}{Hypotenuse} \\

 & =\dfrac{AE}{AD} \\

 & =\dfrac{AG-EG}{AD} \\

 & =\dfrac{AG}{AD}-\dfrac{EG}{AD} \\

\end{align}$

Now multiplying and dividing by AF and DF we get,

$=\dfrac{AG}{AF}\times \dfrac{AF}{AD}-\dfrac{EG}{DF}\times \dfrac{DF}{AD}.......(1)$

Now from $\Delta AFG$ we can find $\cos \theta $

From $\Delta ADF$ we can find $\cos \phi \text{ and sin}\phi $

From $\Delta DHF$ we can find $\sin \theta $

Now using all these values we get,

$\begin{align}

  & \dfrac{AG}{AF}=\cos \theta \\

 & \dfrac{EG}{DF}=\dfrac{HF}{DF}=\sin \theta \\

 & \dfrac{AF}{AD}=\cos \phi \\

 & \dfrac{DF}{AD}=\sin \phi \\

\end{align}$

Now putting these values in (1) we get,

$\cos \left( \theta +\phi \right)=\cos \theta \cos \phi -\sin \theta \sin \phi $

Hence, we have proved the given expression.

Now putting $-\phi $ in place of $\phi $ , we get,

$\cos \left( \theta -\phi \right)=\cos \theta \cos \phi +\sin \theta \sin \phi $

Hence, we have proved the given expression.

Note: It’s always better that we check if the answer that we have got by using the above formula we is correct or not to avoid some calculation mistake and for that we need to put some values in place of $\theta $ and $\phi $ to check whether it satisfies the above expression or not. There are a bunch of trigonometric formulas that should be kept in mind while solving these questions and if we use some different set of formulas then that will be another method to solve this question, but at some point we can see that they are nearly equal.