Question

Prove the following statement: Chords equidistant from the center of the circle are equal in length.

Answer 1

Hint: Let there be a circle and AB and CD be two of its chords which are equidistant from the center O of the circle. Join OA and OC. Draw perpendicular OL and OM from O to AB and CD. Now prove the congruence of triangles ALO and CMO using the RHS congruence rule. Then use CPCT to get $AL = CM$. Multiply this by 2 to get the final answer.

Complete step-by-step solution
In this question, we need to prove that chords equidistant from the center of the circle are equal in length.
Let there be a circle and AB and CD be two of its chords which are equidistant from the center O of the circle.
We need to prove that $AB = CD.$
We will do construction before the proof. Join OA and OC.
Also, draw perpendicular OL from O to AB and perpendicular OM from O to CD.
Proof: The diagram after the construction will look like the following:

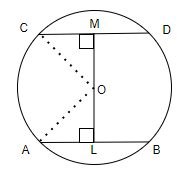
We know the property that the perpendicular from the center of a circle to a chord bisects the chord.
So, using this property, we have the following:
$AL = BL$ and $CM = DM$
Now, we will prove the congruence of the triangles ALO and CMO.
In these triangles,
$OA = OC$ [since OA and OC are radius and radius of a circle remains constant]
$OM = OL$ [we are given that AB and CD are equidistant from the center]
$\angle OLA=\angle OMC=90{}^\circ $ [since OL and OM are perpendiculars from O to AB and CD respectively]
So, by the RHS congruence rule, we have $\Delta ALO\cong \Delta CMO$.
Now using CPCT, we have AL = CM
Multiplying both sides by 2, we will get the following:
$2 AL = 2 CM$
$AB = CD$
Hence proved.

Note: In this question, it is very important to know about the congruence of triangles. Triangles are congruent when all corresponding sides and interior angles are congruent. The triangles will have the same shape and size, but one may be a mirror image of the other. Also, CPCT stands for Corresponding Parts of Congruent Triangles.