Question

Prove the following ${{\text{r}}_{\text{1}}}+{{\text{r}}_{\text{2}}}-{{\text{r}}_{\text{3}}}+\text{r}=\text{4RcosC}$ if r is the radius of in-circle and ${{\text{r}}_{\text{1}}}\text{,}{{\text{r}}_{\text{2}}}\text{,}{{\text{r}}_{\text{3}}}$ are the radius of ex-circles opposite to A, B, C of $\Delta ABC$ respectively.

Answer 1

Hint: At first, substitute $r=\dfrac{\Delta }{s},{{r}_{1}}=\dfrac{\Delta }{s-a},{{r}_{2}}=\dfrac{\Delta }{s-b}\text{ and }{{r}_{3}}=\dfrac{\Delta }{s-c}$ and hence simplify, then use the fact that $2s=a+b+c$. Then use the cosine rule which is \[{{a}^{2}}+{{b}^{2}}-{{c}^{2}}=2ab\cos C\] and substitute it to simplify and get the answer.

Complete step by step answer:

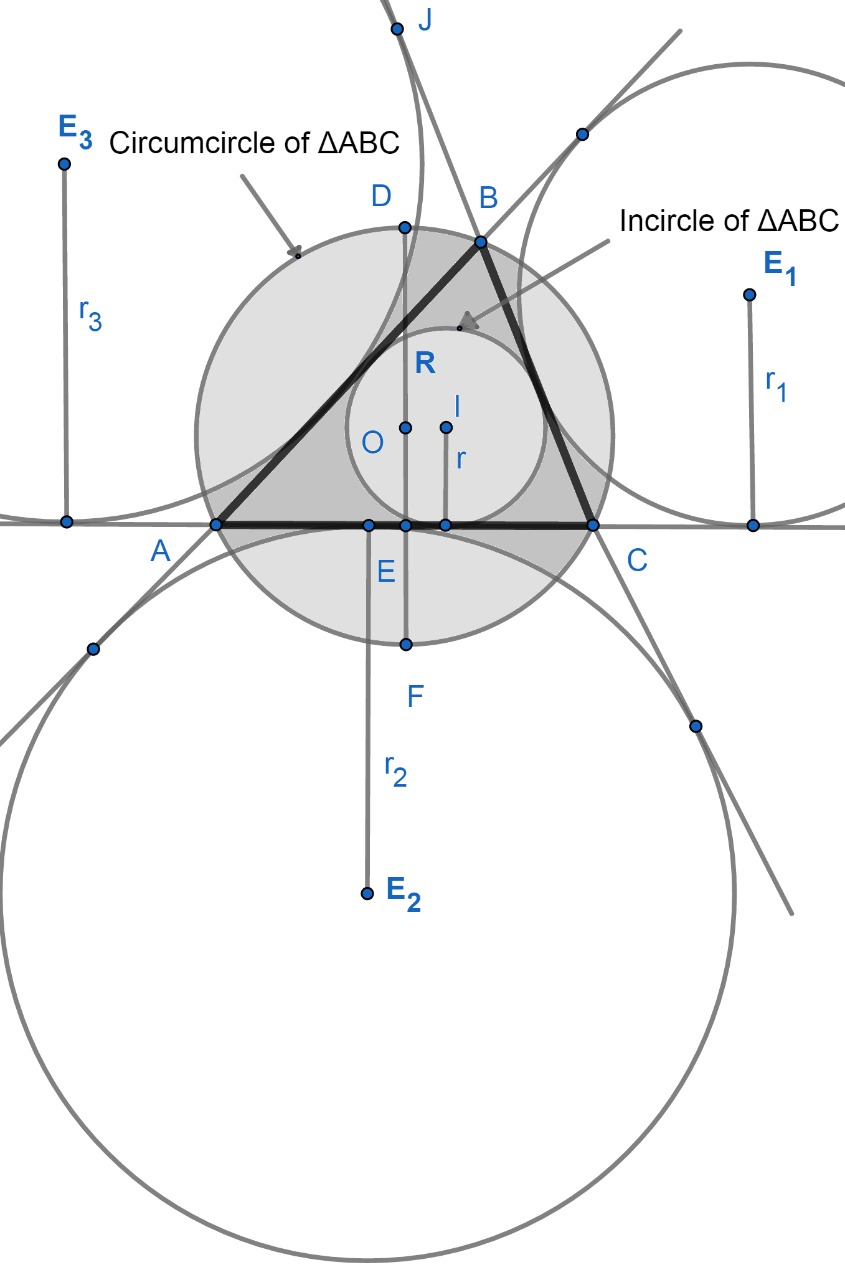
In the question, we are asked to prove that ${{\text{r}}_{\text{1}}}+{{\text{r}}_{\text{2}}}-{{\text{r}}_{\text{3}}}+\text{r}$ is equal to 4RcosC.
If r is radius of in circle and ${{\text{r}}_{\text{1}}}\text{,}{{\text{r}}_{\text{2}}}\text{,}{{\text{r}}_{\text{3}}}$ are radius of ex-circles opposite to A, B, C of $\Delta ABC$ respectively then,
\[r=\dfrac{\Delta }{s},{{r}_{1}}=\dfrac{\Delta }{s-a},{{r}_{2}}=\dfrac{\Delta }{s-b}\text{ and }{{r}_{3}}=\dfrac{\Delta }{s-c}\]
Where, $\Delta =\sqrt{s\left( s-b \right)\left( s-a \right)\left( s-c \right)}$ and s is $\dfrac{a+b+c}{2}$ and also called semi perimeter. Now, using these values we can write ${{\text{r}}_{\text{1}}}+{{\text{r}}_{\text{2}}}-{{\text{r}}_{\text{3}}}+\text{r}$ as,
\[\dfrac{\Delta }{s-a}+\dfrac{\Delta }{s-b}-\dfrac{\Delta }{s-c}+\dfrac{\Delta }{s}\]
Which can be simplified as,
\[\begin{align}
  & \Delta \left( \dfrac{1}{s-a}+\dfrac{1}{s-b} \right)+\Delta \left( \dfrac{1}{s}-\dfrac{1}{s-c} \right) \\
 & \Rightarrow \Delta \left( \dfrac{2s-a-b}{\left( s-a \right)\left( s-b \right)} \right)+\Delta \left( \dfrac{s-c-s}{s\left( s-c \right)} \right) \\
 & \Rightarrow \Delta \left( \dfrac{2s-a-b}{\left( s-a \right)\left( s-b \right)} \right)+\dfrac{\Delta \left( -c \right)}{s\left( s-c \right)} \\
\end{align}\]
Now, as we know $2s=a+b+c$ so we can take $2s-a-b$ as C. So,
\[\dfrac{\Delta c}{\left( s-a \right)\left( s-b \right)}-\dfrac{\Delta c}{s\left( s-c \right)}\]
Which can also be written as,
\[\begin{align}
  & \Delta c\left( \dfrac{1}{\left( s-a \right)\left( s-b \right)}-\dfrac{1}{s\left( s-c \right)} \right) \\
 & \Rightarrow \Delta c\left( \dfrac{s\left( s-c \right)-\left( s-a \right)\left( s-b \right)}{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \right) \\
\end{align}\]
As we know $\Delta =\sqrt{s\left( s-b \right)\left( s-a \right)\left( s-c \right)}$ so, we can write it as,
\[\begin{align}
  & \dfrac{\Delta c}{{{\Delta }^{2}}}\left( {{s}^{2}}-sc-{{s}^{2}}-ab+s\left( a+b \right) \right) \\
 & \Rightarrow \dfrac{c}{\Delta }\left( s\left( a+b+c \right)-ab \right) \\
\end{align}\]
We will substitute s as $\dfrac{a+b+c}{2}$ so we get:
\[\dfrac{c}{\Delta }\left( \dfrac{\left( a+b+c \right)\left( \dfrac{a+b-c}{2} \right)}{2}-ab \right)\]
Which on multiplying we get:
\[\begin{align}
  & \dfrac{c}{\Delta }\left( \dfrac{{{a}^{2}}+2ab+{{b}^{2}}-{{c}^{2}}}{2}-ab \right) \\
 & \Rightarrow \dfrac{c}{2\Delta }\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right) \\
\end{align}\]
Now using cosine rule we can say that,
\[{{a}^{2}}+{{b}^{2}}-{{c}^{2}}=2ab\cos C\]
So we get:
\[\begin{align}
  & \dfrac{c}{2\Delta }\times 2ab\cos C \\
 & \Rightarrow \left( \dfrac{abc}{\Delta } \right)\cos C \\
\end{align}\]
Here, we will use a formula which states that $\Delta =\dfrac{abc}{4R}\Rightarrow 4R=\dfrac{abc}{\Delta }$ so we can say that,
$\left( \dfrac{abc}{\Delta } \right)\cos C$ equals 4RcosC.
Hence, ${{\text{r}}_{\text{1}}}+{{\text{r}}_{\text{2}}}-{{\text{r}}_{\text{3}}}+\text{r}$ equals to 4RcosC is proved.

Note: Students generally solving out or providing these kinds of problems tend to forget or make mistakes while writing formulas. So, they should be careful about it, otherwise the solution might get wrong.