Question

Prove the following expression, $\tan \left( -225{}^\circ \right)\cot \left( -405{}^\circ \right)-\tan \left( -765{}^\circ \right)\cot \left( 675{}^\circ \right)=0$.

Answer 1

Hint: We have to prove that the value of the given expression is 0. For that, we can see that the angles are not standard angles whose values are known to us. So, we have to first use formulas to convert them into standard forms. We can use formulas, $\tan \left( -x \right)=-\tan x,\cot \left( -x \right)=-\cot x$ and also represent the angles such that they are in the form (180 +/- 45) or (360 +/- 45) to get the value of the angles.

Complete step-by-step answer:

It is given in the question that we have to prove the expression, $\tan \left( -225{}^\circ \right)\cot \left( -405{}^\circ \right)-\tan \left( -765{}^\circ \right)\cot \left( 675{}^\circ \right)=0$. For that, we will consider the left hand side or the LHS first. We know that, $\tan \left( -x \right)=-\tan x,\cot \left( -x \right)=-\cot x$, so applying that in the given expression, we get, LHS as,

$=-\tan \left( 225{}^\circ \right)-\cot \left( 405{}^\circ \right)+\tan \left( 765{}^\circ \right)\cot \left( 675{}^\circ \right)$

Now, we will solve each of the angles individually. So, we get,

$\begin{align}

  & -\tan \left( 225{}^\circ \right)=-\tan \left( 90{}^\circ \times 2+45{}^\circ \right) \\

 & =-\tan \left( 180{}^\circ +45{}^\circ \right) \\

\end{align}$

We know that, $\tan \left( 180{}^\circ +\theta \right)=\tan \theta $, so by applying that in the above expression, we get,

$=-\tan 45{}^\circ =-1$

Similarly, we get,

$\begin{align}

  & -\cot \left( 405{}^\circ \right)=-\cot \left( 90{}^\circ \times 4+45{}^\circ \right) \\

 & =-\cot \left( 360{}^\circ +45{}^\circ \right) \\

\end{align}$

We know that, $\cot \left( 360{}^\circ +\theta \right)=\cot \theta $, so, we get,

$=-\cot 45{}^\circ =-1$

Let us consider the quadrants first,

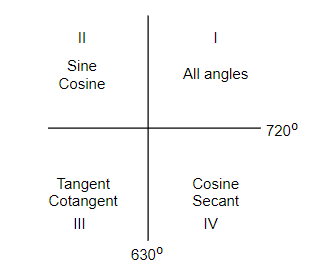
Then, we can write,

$\begin{align}

  & \tan \left( 765{}^\circ \right)=\tan \left( 90{}^\circ \times 8+45{}^\circ \right) \\

 & =\tan \left( 720{}^\circ +45{}^\circ \right) \\

\end{align}$

Considering the quadrant, we know that tan is positive in the first and third quadrant. So, $720{}^\circ +\theta $ indicates an angle in the first quadrant, so we get, $\tan \left( 720{}^\circ +45{}^\circ \right)=\tan 45{}^\circ $. So, we get, $=\tan 45{}^\circ =1$

And finally, we get,

$\begin{align}

  & \cot \left( 675{}^\circ \right)=\cot \left( 90{}^\circ \times 7+45{}^\circ \right) \\

 & =\cot \left( 630{}^\circ +45{}^\circ \right) \\

\end{align}$

Considering the quadrant, we know that cot is positive in the first and third quadrant. So, $630{}^\circ +\theta $ indicates an angle in the fourth quadrant, so we get, $\cot \left( 630{}^\circ +45{}^\circ \right)=-\cot 45{}^\circ $. So, we get,

$=-\cot 45{}^\circ =-1$

Now, putting all the obtained values in the expression, we get,

$\begin{align}

  & =\left( -1 \right)\times \left( -1 \right)+\left( 1 \right)\times \left( -1 \right) \\

 & =1-1 \\

 & =0 \\

\end{align}$

Which is the same as the value of the right hand side or RHS of given expression. Therefore, LHS = RHS.

Hence, we have proved that the value of the given expression is 0.


Note: The students usually make a mistake with the plus and minus signs of the angles, while doing the conversions. Therefore, it is advisable to do the conversions step by step to avoid the chances of error.