Question

Prove the following:
${\cos ^2}2x - {\cos ^2}6x = \sin 4x\sin 8x$

Answer 1

Hint: We can take the LHS of the given equation and factorize it using the equation ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$. Then we can simplify it using the trigonometric identities \[\cos \left( A \right) + \cos \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)\]and\[\cos \left( A \right) - \cos \left( B \right) = - 2\sin \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)\]. On simplification and further calculations, we will obtain the RHS of the equation. When $LHS = RHS$ we can say that the given equation is correct.

Complete step by step Answer:

We need to prove that ${\cos ^2}2x - {\cos ^2}6x = \sin 4x\sin 8x$
Let us look at the LHS.
$LHS = {\cos ^2}2x - {\cos ^2}6x$
It is of the form ${a^2} - {b^2}$
We know that ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$
We can substitute the values,
 $ \Rightarrow {\cos ^2}2x - {\cos ^2}6x = \left( {\cos 2x + \cos 6x} \right)\left( {\cos 2x - \cos 6x} \right)$
Then the LHS becomes,
\[ \Rightarrow LHS = \left( {\cos 2x + \cos 6x} \right)\left( {\cos 2x - \cos 6x} \right)\] … (1)
We know that \[\cos \left( A \right) + \cos \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)\]
We can substitute the values,
\[ \Rightarrow \left( {\cos 2x + \cos 6x} \right) = 2\cos \left( {\dfrac{{2x + 6x}}{2}} \right)\cos \left( {\dfrac{{2x - 6x}}{2}} \right)\]
On simplification, we get,
\[ \Rightarrow \left( {\cos 2x + \cos 6x} \right) = 2\cos \left( {4x} \right)\cos \left( { - 2x} \right)\]
We know that \[\cos \left( { - x} \right) = \cos \left( x \right)\]. So, we get,
\[ \Rightarrow \left( {\cos 2x + \cos 6x} \right) = 2\cos \left( {4x} \right)\cos \left( {2x} \right)\] … (2)
We know that \[\cos \left( A \right) - \cos \left( B \right) = - 2\sin \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)\]
We can substitute the values,
\[ \Rightarrow \left( {\cos 2x - \cos 6x} \right) = - 2\sin \left( {\dfrac{{2x + 6x}}{2}} \right)\sin \left( {\dfrac{{2x - 6x}}{2}} \right)\]
On simplification, we get,
\[ \Rightarrow \left( {\cos 2x - \cos 6x} \right) = - 2\sin \left( {4x} \right)\sin \left( { - 2x} \right)\]
We know that \[\sin \left( { - x} \right) = - \sin \left( x \right)\]. So, we get,
\[ \Rightarrow \left( {\cos 2x - \cos 6x} \right) = 2\sin \left( {4x} \right)\sin \left( {2x} \right)\] … (3)
Substituting (3) and (2) in (1), we get,
\[ \Rightarrow LHS = \left( {2\cos 4x\cos 2x} \right)\left( {2\sin 4x\sin 2x} \right)\]
On rearranging, we get,
\[ \Rightarrow LHS = \left( {2\sin 2x\cos 2x} \right)\left( {2\sin 4x\cos 4x} \right)\]
We know that $\sin 2A = 2\sin A\cos A$
\[ \Rightarrow LHS = \sin 4x\sin 8x\]
RHS is also equal to\[\sin 4x\sin 8x\]. So, we can write,
$LHS = RHS$.
Hence the equation is proved.

Note: We must be familiar to the following trigonometric identities used in this problem.
\[\cos \left( A \right) + \cos \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)\]
\[\cos \left( A \right) - \cos \left( B \right) = - 2\sin \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)\]
\[\sin \left( { - x} \right) = - \sin \left( x \right)\]
\[\cos \left( { - x} \right) = \cos \left( x \right)\]
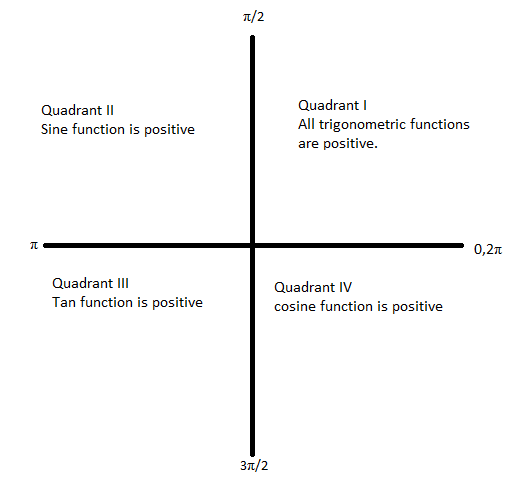
We must know the values of trigonometric functions at common angles. Adding $\pi $ or multiples of $\pi $with the angle retains the ratio and adding $\dfrac{\pi }{2}$ or odd multiples of $\dfrac{\pi }{2}$ will change the ratio. While converting the angles we must take care of the sign of the ratio in its respective quadrant. In the 1^st quadrant all the trigonometric ratios are positive. In the 2^nd quadrant only sine and sec are positive. In the third quadrant, only tan and cot are positive and in the fourth quadrant, only cos and sec are positive. The following figure gives us an idea about the signs of different trigonometric functions. The angle measured in the counter clockwise direction is taken as positive and angle measured in the clockwise direction is taken as negative.