Question

Prove the converse of the mid-point theorem following the guidelines given below:
Consider a triangle ABC with D as the midpoint of AB. Draw DE|| BC to intersect AC in E. Let ${{\text{E}}_1}$ be the midpoint of AC. Use mid-point theorem to get ${{\text{DE}}_1}$|| BC and ${{\text{DE}}_1}=\dfrac{1}{2}$BC. Conclude $E={{\text{E}}_1}$ and hence E is the midpoint of AC.

Answer 1

Hint: First we will make the diagram from the information given in the question. After that we will use the property of similar triangles that corresponding sides of two similar triangles are proportional to each other and then put the value of sides in the equation obtained to get the midpoint of side AC.

Complete step-by-step answer:
The diagram for the question is given below:

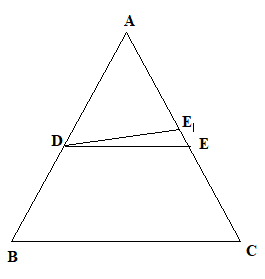
It is given that:
DE||BC
D is the midpoint of side AB.
And ${{\text{E}}_1}$is the mid- point of the side AC.
We have to prove that E=${{\text{E}}_1}$
In $\vartriangle $ABC and $\vartriangle $ADE, we have:
$\angle $ABC = $\angle $ADE ( By corresponding angle)
$\angle $ACB = $\angle $AED (By corresponding angle)
 $\angle $BAC = $\angle $DAE (Common angle)
$\because $ All the angles of $\vartriangle $ABC is equal to corresponding angles of $\vartriangle $ADE.
So, by AAA rule of similarity, both the triangles are similar i.e.
$\vartriangle $ABC$ \sim $ $\vartriangle $ADE
We know that if two triangles are similar then their corresponding sides are proportional to each other.
Therefore, we can write:
$
  \dfrac{{{\text{AB}}}}{{{\text{AD}}}} = \dfrac{{{\text{AC}}}}{{{\text{AE}}}} = \dfrac{{{\text{BC}}}}{{{\text{DE}}}} \\
   \Rightarrow \dfrac{{{\text{AB}}}}{{{\text{AD}}}} = \dfrac{{{\text{AC}}}}{{{\text{AE}}}} \\
 $ ----(1)
$ \Rightarrow \dfrac{{{\text{AB}}}}{{{\text{AD}}}} = \dfrac{{{\text{BC}}}}{{{\text{DE}}}}$ -------(2)
$\because $It is given that D is the midpoint of AB.
$\therefore $ AB = 2AD ----- (3)
Putting this value in equation 1, we get:
$\dfrac{{2{\text{AD}}}}{{{\text{AD}}}} = \dfrac{{{\text{AC}}}}{{{\text{AE}}}}$
$ \Rightarrow $ AC = 2AE
$\therefore $ E is the midpoint of AC
But it is given that ${{\text{E}}_1}$is the mid- point of AC.
Therefore, we can say that E=${{\text{E}}_1}$.
Now, using equation 2 and 3, we get:
$\dfrac{{2{\text{AD}}}}{{{\text{AD}}}} = \dfrac{{{\text{BC}}}}{{{\text{DE}}}}$
$ \Rightarrow $ BC = 2DE.
$ \Rightarrow $DE=$\dfrac{1}{2}$BC.
Therefore, it is proved that DE=$\dfrac{1}{2}$BC.

Note: First important thing is that in the question involving geometry specially proof, you must draw a diagram. It will give you a clear path to proceed. In this question, the important step is the use of the concept of similar triangles. You should know that if DE=$\dfrac{1}{2}$BC then DE|| BC. This is called the mid-point theorem.