
Prove that two of the lines represented by the following equation:
$a{{y}^{4}}+bx{{y}^{3}}+c{{x}^{2}}{{y}^{2}}+d{{x}^{3}}y+e{{x}^{4}}=0$ will be perpendicular if,
$\left( b+d \right)\left( ad+be \right)+{{\left( e-a \right)}^{2}}\left( a+c+e \right)=0$
Answer
585k+ views
Hint: As you can see the equation given in the above problem is of degree 4 meaning this equation is representing the combination of 4 straight lines. First of all, draw two lines which are perpendicular and we know that if two lines are perpendicular then the relation between their slopes is ${{m}_{1}}{{m}_{2}}=-1$. And let us assume the slopes of other lines are ${{m}_{3}}\And {{m}_{4}}$. Then the given equation is a homogeneous equation so the combined equation of two perpendicular lines is also a homogeneous equation. So, write the combined homogeneous equation and find the roots of the equation are ${{m}_{1}}\And {{m}_{2}}$ so write the product of the roots in terms of the two perpendicular lines. Similarly, write the equation for the remaining two straight lines which are not perpendicular and write the sum and product of the roots. After that multiply all the 4 straight lines and compare with the given equation and hence, find the relation between the coefficients of the given equation.
Complete step by step answer:
We have given the following equation:
$a{{y}^{4}}+bx{{y}^{3}}+c{{x}^{2}}{{y}^{2}}+d{{x}^{3}}y+e{{x}^{4}}=0$
The above equation is of degree 4, it means this equation is formed from the 4 straight lines. It is given that two of the straight lines are perpendicular so in the below figure, we have drawn two lines perpendicular to each other and the other two lines which are not.
As you can see that the above equation is a homogeneous equation meaning all the 4 straight lines are passing through the origin.
In the below figure, we have shown two perpendicular lines by AB and CD and the remaining two straight lines by EF and GH.
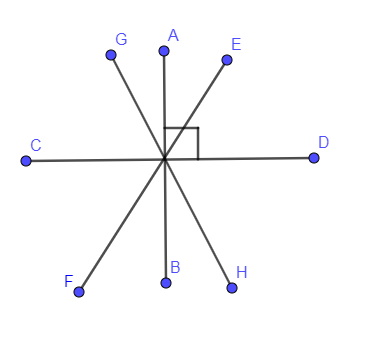
As AB and CD are perpendicular to each other so if one line is having slope ${{m}_{1}}$ then the slope of the other line is $-\dfrac{1}{{{m}_{1}}}$ because the product of the two perpendicular lines is -1.
Now, we can write the homogeneous equation of these two perpendicular lines as follows:
$a'{{y}^{2}}+2h'xy+f'{{x}^{2}}=0$
Let us divide the above equation by ${{x}^{2}}$ we get,
$\begin{align}
& \dfrac{a'{{y}^{2}}}{{{x}^{2}}}+\dfrac{2h'xy}{{{x}^{2}}}+\dfrac{f'{{x}^{2}}}{{{x}^{2}}}=0 \\
& \Rightarrow a'\left( \dfrac{{{y}^{2}}}{{{x}^{2}}} \right)+2h'\left( \dfrac{y}{x} \right)+f'=0 \\
\end{align}$
We can write $\dfrac{y}{x}$ as m in the above equation.
$a'{{m}^{2}}+2h'm+f'=0$ ………… Eq. (1)
The roots of the above equation are equal to:
${{m}_{1}}\And -\dfrac{1}{{{m}_{1}}}$
So, product of the roots is equal to:
$\begin{align}
& -1=\dfrac{f'}{a'} \\
& \Rightarrow f'=-a' \\
\end{align}$
Substituting the above value in eq. (1) we get,
$a'{{m}^{2}}+2h'm-a'=0$……. Eq. (2)
Similarly, we can write the equation for the remaining two straight lines which are not perpendicular to each other as follows:
$b'{{m}^{2}}+c'm+d'=0$ ……… Eq. (3)
Let us assume the slope of these lines as ${{m}_{2}}\And {{m}_{3}}$.
Multiplying eq. (2) and eq. (3) will give the combined equation of degree 4.
$\begin{align}
& \left( a'{{m}^{2}}+2h'm-a' \right)\left( b'{{m}^{2}}+c'm+d' \right)=0 \\
& \Rightarrow a'b'{{m}^{4}}+a'c'{{m}^{3}}+a'd'{{m}^{2}}+2h'b'{{m}^{3}}+2h'c'{{m}^{2}}+2h'd'm-a'b'{{m}^{2}}-a'c'm-a'd'=0 \\
& \Rightarrow a'b'{{m}^{4}}+\left( a'c'+2h'b' \right){{m}^{3}}+\left( a'd'+2h'c'-a'b' \right){{m}^{2}}+\left( 2h'd'-a'c' \right)m-a'd'=0.......Eq.(4) \\
\end{align}$
The equation given in the above is equal to:
$a{{y}^{4}}+bx{{y}^{3}}+c{{x}^{2}}{{y}^{2}}+d{{x}^{3}}y+e{{x}^{4}}=0$
Dividing ${{x}^{4}}$ in the above equation we get,
$a{{\left( \dfrac{y}{x} \right)}^{4}}+b{{\left( \dfrac{y}{x} \right)}^{3}}+c{{\left( \dfrac{y}{x} \right)}^{2}}+d\left( \dfrac{y}{x} \right)+e=0$
We can write $\dfrac{y}{x}$ as m in the above equation.
$a{{\left( m \right)}^{4}}+b{{\left( m \right)}^{3}}+c{{\left( m \right)}^{2}}+d\left( m \right)+e=0$………. Eq. (5)
Comparing eq. (4) by eq. (5) we get,
$\begin{align}
& a'b'=a \\
& a'c'+2h'b'=b \\
& a'd'+2h'c'-a'b'=c \\
& 2h'd'-a'c'=d \\
& -a'd'=e \\
\end{align}$
Now, to prove the above equation and the equation is as follows:
$\left( b+d \right)\left( ad+be \right)+{{\left( e-a \right)}^{2}}\left( a+c+e \right)=0$…….. Eq. (6)
First of all we are writing the terms given in the brackets as follows:
$\begin{align}
& b+d=a'c'+2h'b'+2h'd'-a'c' \\
& \Rightarrow b+d=2h'\left( b'+d' \right) \\
\end{align}$
$\begin{align}
& ad+be=a'b'\left( 2h'd'-a'c' \right)-\left( a'c'+2h'b' \right)a'd' \\
& \Rightarrow ad+be=a'b'2h'd'-a'b'\left( a'c' \right)-a'c'\left( a'd' \right)-2h'b'a'd' \\
& \Rightarrow ad+be=-a'c'\left( a'b'+a'd' \right) \\
\end{align}$
$\begin{align}
& {{\left( e-a \right)}^{2}}={{\left( -a'd'-a'b' \right)}^{2}} \\
& \Rightarrow {{\left( e-a \right)}^{2}}={{\left( a'd'+a'b' \right)}^{2}} \\
& a+c+e=a'b'+a'd'+2h'c'-a'b'-a'd' \\
& \Rightarrow a+c+e=2h'c' \\
\end{align}$
Now, substituting these bracket simplifications in eq. (6) we get,
$\begin{align}
& -a'c'\left( 2h'\left( b'+d' \right) \right)\left( a'b'+a'd' \right)+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
& \Rightarrow -c'2h'\left( a'b'+a'd' \right)\left( a'b'+a'd' \right)+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
& \Rightarrow -2h'c'{{\left( a'd'+a'b' \right)}^{2}}+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
\end{align}$
Taking ${{\left( a'd'+a'b' \right)}^{2}}$ as common from the L.H.S of the above equation we get,
$\begin{align}
& {{\left( a'd'+a'b' \right)}^{2}}\left( -2h'c'+2h'c' \right)=0 \\
& \Rightarrow 0=0 \\
\end{align}$
From the above, we got L.H.S is equal to R.H.S of eq. (6). Hence, we have proved.
Note:
The question demands the knowledge of a homogeneous equation and the condition for two lines to be perpendicular. Apart from that you also should know that if a 4-degree equation is given and we are talking about the straight lines then that 4 degree equation is constructed by multiplying the 4 straight line equations altogether. Lacking any of the information will inhibit you from moving forward in this problem.
Complete step by step answer:
We have given the following equation:
$a{{y}^{4}}+bx{{y}^{3}}+c{{x}^{2}}{{y}^{2}}+d{{x}^{3}}y+e{{x}^{4}}=0$
The above equation is of degree 4, it means this equation is formed from the 4 straight lines. It is given that two of the straight lines are perpendicular so in the below figure, we have drawn two lines perpendicular to each other and the other two lines which are not.
As you can see that the above equation is a homogeneous equation meaning all the 4 straight lines are passing through the origin.
In the below figure, we have shown two perpendicular lines by AB and CD and the remaining two straight lines by EF and GH.

As AB and CD are perpendicular to each other so if one line is having slope ${{m}_{1}}$ then the slope of the other line is $-\dfrac{1}{{{m}_{1}}}$ because the product of the two perpendicular lines is -1.
Now, we can write the homogeneous equation of these two perpendicular lines as follows:
$a'{{y}^{2}}+2h'xy+f'{{x}^{2}}=0$
Let us divide the above equation by ${{x}^{2}}$ we get,
$\begin{align}
& \dfrac{a'{{y}^{2}}}{{{x}^{2}}}+\dfrac{2h'xy}{{{x}^{2}}}+\dfrac{f'{{x}^{2}}}{{{x}^{2}}}=0 \\
& \Rightarrow a'\left( \dfrac{{{y}^{2}}}{{{x}^{2}}} \right)+2h'\left( \dfrac{y}{x} \right)+f'=0 \\
\end{align}$
We can write $\dfrac{y}{x}$ as m in the above equation.
$a'{{m}^{2}}+2h'm+f'=0$ ………… Eq. (1)
The roots of the above equation are equal to:
${{m}_{1}}\And -\dfrac{1}{{{m}_{1}}}$
So, product of the roots is equal to:
$\begin{align}
& -1=\dfrac{f'}{a'} \\
& \Rightarrow f'=-a' \\
\end{align}$
Substituting the above value in eq. (1) we get,
$a'{{m}^{2}}+2h'm-a'=0$……. Eq. (2)
Similarly, we can write the equation for the remaining two straight lines which are not perpendicular to each other as follows:
$b'{{m}^{2}}+c'm+d'=0$ ……… Eq. (3)
Let us assume the slope of these lines as ${{m}_{2}}\And {{m}_{3}}$.
Multiplying eq. (2) and eq. (3) will give the combined equation of degree 4.
$\begin{align}
& \left( a'{{m}^{2}}+2h'm-a' \right)\left( b'{{m}^{2}}+c'm+d' \right)=0 \\
& \Rightarrow a'b'{{m}^{4}}+a'c'{{m}^{3}}+a'd'{{m}^{2}}+2h'b'{{m}^{3}}+2h'c'{{m}^{2}}+2h'd'm-a'b'{{m}^{2}}-a'c'm-a'd'=0 \\
& \Rightarrow a'b'{{m}^{4}}+\left( a'c'+2h'b' \right){{m}^{3}}+\left( a'd'+2h'c'-a'b' \right){{m}^{2}}+\left( 2h'd'-a'c' \right)m-a'd'=0.......Eq.(4) \\
\end{align}$
The equation given in the above is equal to:
$a{{y}^{4}}+bx{{y}^{3}}+c{{x}^{2}}{{y}^{2}}+d{{x}^{3}}y+e{{x}^{4}}=0$
Dividing ${{x}^{4}}$ in the above equation we get,
$a{{\left( \dfrac{y}{x} \right)}^{4}}+b{{\left( \dfrac{y}{x} \right)}^{3}}+c{{\left( \dfrac{y}{x} \right)}^{2}}+d\left( \dfrac{y}{x} \right)+e=0$
We can write $\dfrac{y}{x}$ as m in the above equation.
$a{{\left( m \right)}^{4}}+b{{\left( m \right)}^{3}}+c{{\left( m \right)}^{2}}+d\left( m \right)+e=0$………. Eq. (5)
Comparing eq. (4) by eq. (5) we get,
$\begin{align}
& a'b'=a \\
& a'c'+2h'b'=b \\
& a'd'+2h'c'-a'b'=c \\
& 2h'd'-a'c'=d \\
& -a'd'=e \\
\end{align}$
Now, to prove the above equation and the equation is as follows:
$\left( b+d \right)\left( ad+be \right)+{{\left( e-a \right)}^{2}}\left( a+c+e \right)=0$…….. Eq. (6)
First of all we are writing the terms given in the brackets as follows:
$\begin{align}
& b+d=a'c'+2h'b'+2h'd'-a'c' \\
& \Rightarrow b+d=2h'\left( b'+d' \right) \\
\end{align}$
$\begin{align}
& ad+be=a'b'\left( 2h'd'-a'c' \right)-\left( a'c'+2h'b' \right)a'd' \\
& \Rightarrow ad+be=a'b'2h'd'-a'b'\left( a'c' \right)-a'c'\left( a'd' \right)-2h'b'a'd' \\
& \Rightarrow ad+be=-a'c'\left( a'b'+a'd' \right) \\
\end{align}$
$\begin{align}
& {{\left( e-a \right)}^{2}}={{\left( -a'd'-a'b' \right)}^{2}} \\
& \Rightarrow {{\left( e-a \right)}^{2}}={{\left( a'd'+a'b' \right)}^{2}} \\
& a+c+e=a'b'+a'd'+2h'c'-a'b'-a'd' \\
& \Rightarrow a+c+e=2h'c' \\
\end{align}$
Now, substituting these bracket simplifications in eq. (6) we get,
$\begin{align}
& -a'c'\left( 2h'\left( b'+d' \right) \right)\left( a'b'+a'd' \right)+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
& \Rightarrow -c'2h'\left( a'b'+a'd' \right)\left( a'b'+a'd' \right)+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
& \Rightarrow -2h'c'{{\left( a'd'+a'b' \right)}^{2}}+{{\left( a'd'+a'b' \right)}^{2}}\left( 2h'c' \right)=0 \\
\end{align}$
Taking ${{\left( a'd'+a'b' \right)}^{2}}$ as common from the L.H.S of the above equation we get,
$\begin{align}
& {{\left( a'd'+a'b' \right)}^{2}}\left( -2h'c'+2h'c' \right)=0 \\
& \Rightarrow 0=0 \\
\end{align}$
From the above, we got L.H.S is equal to R.H.S of eq. (6). Hence, we have proved.
Note:
The question demands the knowledge of a homogeneous equation and the condition for two lines to be perpendicular. Apart from that you also should know that if a 4-degree equation is given and we are talking about the straight lines then that 4 degree equation is constructed by multiplying the 4 straight line equations altogether. Lacking any of the information will inhibit you from moving forward in this problem.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




