Question

Prove that the velocity of the lower end of the vertical rod in order to complete the vertical circle about its one end should be $\sqrt {6gl} $ where l is the length of the rod.

Answer 1

Hint: There is one law which will be valid anywhere and at any situation universally and that law is law of conservation of energy. That means energy can neither be created nor destroyed but it is only converted from one form to the other. By using this law we will solve this problem.

Formula used:
Formula used:
$P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f}$
$U = mgh$

Complete step by step answer:
When we do any work against the conservative force then the work done by us will be stored in the form of potential energy in the system and potential energy increases. Along the direction of conservative force then potential energy of the system decreases.
Here in this problem the rod will be rotating from the vertical position in the bottom to the vertical position on the top about the other end. That means the center of mass of the rod is moving in a vertically upward direction. Potential energy is gained as it is moving opposite to the conservative gravitational force.
If potential energy is gained, as energy can neither be created nor destroyed some other energy must be lost. There are no energies involved here except potential and kinetic energies. Hence the initial rotational kinetic energy is lost and converted to potential energy.
From the below diagram we can see that initially at lower level its has angular velocity $\omega $ so that it has rotational kinetic energy $\dfrac{1}{2}I{\omega ^2}$ and converted to gain in potential energy $mgl$

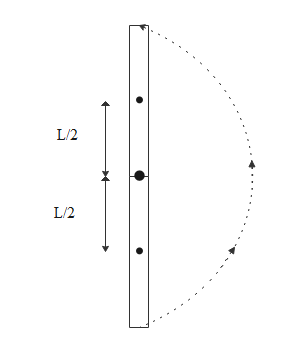
If we apply the mechanical energy conservation we will get
$P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f}$
Potential energy is given as $U = mgh$
$\eqalign{
  & - mg\dfrac{l}{2} + \dfrac{1}{2}I{\omega ^2} = mg\dfrac{l}{2} + 0 \cr
  & \Rightarrow \dfrac{1}{2}I{\omega ^2} = mgl \cr
  & \Rightarrow \dfrac{1}{2}\left( {\dfrac{{m{l^2}}}{3}} \right){\omega ^2} = mgl \cr
  & \Rightarrow \omega = \sqrt {\dfrac{{6g}}{l}} \cr
  & \Rightarrow v = l\omega \cr
  & \Rightarrow v = l\sqrt {\dfrac{{6g}}{l}} \cr
  & \therefore v = \sqrt {6gl} \cr} $
Hence proved.

Note:
When calculating the potential energies we considered half the length of the rod because the center of mass of rod lies there only. We assume the entire mass of the rod is concentrated there and moving up to gain potential energy. It is also assumed that as soon as the tip reaches the highest point its velocity becomes zero, hence the final kinetic energy is assumed to be zero. We assume this because they asked us the minimum velocity of the tip at the lowest point.