Question

Prove that the two parabolas, having the same focus and their axes at opposite directions, cut at right angles.

Answer 1

Hint: The two parabolas of same focus \[\left( a,0 \right)\] having opposite axes are shown in the below figure.

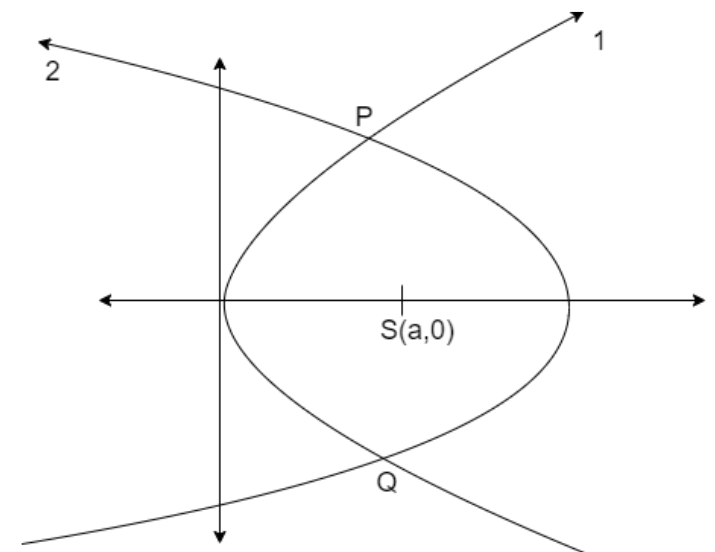
We assume that the equation of the first parabola as \[{{y}^{2}}=4ax\] then the equation of parabola having same focus but the opposite axis is given as \[{{y}^{2}}=-4a\left( x-2a \right)\] then we find the slopes of tangents of both curves at the intersection point so as to prove the product of tangents at intersection point equal to -1 which proves that the curves cut at right angles.

Complete step-by-step solution:
Let us assume that the equation of the first parabola as
\[\Rightarrow {{y}^{2}}=4ax....equation(i)\]
Then we know that the equation of parabola having the same focus but opposite direction of the axis is given as
\[\Rightarrow {{y}^{2}}=-4a\left( x-2a \right)........equation(ii)\]
Now, let us assume that the point of intersection of both the curves as P
Let us find the point P by solving both the equations of parabolas.
By combining both the equations of parabolas we get
\[\begin{align}
  & \Rightarrow 4ax=-4a\left( x-2a \right) \\
 & \Rightarrow 2ax=2a \\
 & \Rightarrow x=a \\
\end{align}\]
By substituting the value of \['x'\] in equation (i) we get
\[\begin{align}
  & \Rightarrow {{y}^{2}}=4a\left( a \right) \\
 & \Rightarrow y=\pm 2a \\
\end{align}\]
Here, we can see that for each value of \['y'\] we get two points of intersection.
Let us assume that one point as \[P\left( a,2a \right)\]
Now let us find the slopes of tangents of two curves at point \[P\left( a,2a \right)\]
Let us assume that the slope of tangent of equation (i) at \[P\left( a,2a \right)\] as \[{{m}_{1}}\] given as \[\dfrac{dy}{dx}\]
By taking the equation (i) and differentiating with respect to \['x'\] we get
\[\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)\]
\[\begin{align}
  & \Rightarrow 2y\dfrac{dy}{dx}=4a \\
 & \Rightarrow {{m}_{1}}=\dfrac{2a}{y} \\
\end{align}\]
Now, by substituting the point \[P\left( a,2a \right)\] in above equation we get
\[\begin{align}
  & \Rightarrow {{m}_{1}}=\dfrac{2a}{2a} \\
 & \Rightarrow {{m}_{1}}=1 \\
\end{align}\]
Let us assume that the slope of tangent of equation (ii) at \[P\left( a,2a \right)\] as \[{{m}_{2}}\]given as \[\dfrac{dy}{dx}\]
By taking the equation (ii) and differentiating with respect to \['x'\] we get
\[\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( -4ax+8{{a}^{2}} \right)\]
\[\begin{align}
  & \Rightarrow 2y\dfrac{dy}{dx}=-4a \\
 & \Rightarrow {{m}_{2}}=-\dfrac{2a}{y} \\
\end{align}\]
Now, by substituting the point \[P\left( a,2a \right)\] in above equation we get
\[\begin{align}
  & \Rightarrow {{m}_{2}}=-\dfrac{2a}{2a} \\
 & \Rightarrow {{m}_{2}}=-1 \\
\end{align}\]
Now, let us find the product of slopes of tangents of both curves we get
\[\Rightarrow {{m}_{1}}\times {{m}_{2}}=-1\]
Here, we can see that the product of slopes of tangents at the point of intersection is -1
Therefore we can conclude that the curves cut at right angles.
Hence the required result has been proved.

Note: We can solve the above result using the other point also that is \[Q\left( a,-2a \right)\]
Now let us find the slopes of tangents of two curves at point \[Q\left( a,-2a \right)\]
Let us assume that the slope of tangent of equation (i) at \[Q\left( a,-2a \right)\] as \[{{m}_{1}}\] given as \[\dfrac{dy}{dx}\]
By taking the equation (i) and differentiating with respect to \['x'\] we get
\[\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)\]
\[\begin{align}
  & \Rightarrow 2y\dfrac{dy}{dx}=4a \\
 & \Rightarrow {{m}_{1}}=\dfrac{2a}{y} \\
\end{align}\]
Now, by substituting the point \[Q\left( a,-2a \right)\] in above equation we get
\[\begin{align}
  & \Rightarrow {{m}_{1}}=\dfrac{2a}{\left( -2a \right)} \\
 & \Rightarrow {{m}_{1}}=-1 \\
\end{align}\]
Let us assume that the slope of tangent of equation (ii) at \[Q\left( a,-2a \right)\] as \[{{m}_{2}}\] given as \[\dfrac{dy}{dx}\]
By taking the equation (ii) and differentiating with respect to \['x'\] we get
\[\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( -4ax+8{{a}^{2}} \right)\]
\[\begin{align}
  & \Rightarrow 2y\dfrac{dy}{dx}=-4a \\
 & \Rightarrow {{m}_{2}}=-\dfrac{2a}{y} \\
\end{align}\]
Now, by substituting the point \[Q\left( a,-2a \right)\] in above equation we get
\[\begin{align}
  & \Rightarrow {{m}_{2}}=-\dfrac{2a}{\left( -2a \right)} \\
 & \Rightarrow {{m}_{2}}=1 \\
\end{align}\]
Now, let us find the product of slopes of tangents of both curves we get
\[\Rightarrow {{m}_{1}}\times {{m}_{2}}=-1\]
Here, we can see that the product of slopes of tangents at the point of intersection is -1
Therefore we can conclude that the curves cut at right angles.
Hence the required result has been proved.