Question

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Answer 1

Hint: Tangents from the same external point on the circle are equal in length; also the radius of a circle makes a right angle with the tangent from any external point.
Complete Step by Step Solution:
Let us try to draw the figure of the circle along with the tangents

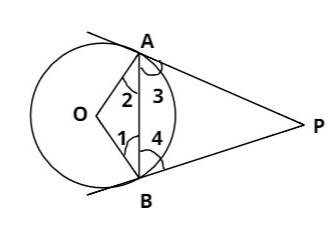
So all we need to do is to prove that angle 3 is equal to angle 4.
Now in this question and figure we are given that A circle with center O, PA and PB are tangents drawn at the ends of AB.
We need to prove that \[\angle PAB = \angle PBA\]
Construction is required by joining OA and OB.
In \[\vartriangle OAB\] we have
\[\begin{array}{l}
OA = OB.............................................(i)\\
\angle 2 = \angle 1..............................................(ii)\\
\left( {\angle 2 + \angle 3} \right) = \left( {\angle 1 + \angle 4} \right)..................................(iii)
\end{array}\]
For (i) it is radii of the the same circle
For (ii) the angle opposite to equal sides of the triangle
For (iii) both \[{90^ \circ }\] as radius is perpendicular to the tangent.
Subtracting (ii) from (iii) we will get it as
\[\begin{array}{l}
\therefore \left( {\angle 2 + \angle 3 - \angle 2} \right) = \left( {\angle 1 + \angle 4 - \angle 1} \right)\\
 \Rightarrow \angle 3 = \angle 4\\
 \Rightarrow \angle PAB = \angle PBA\\
\end{array}\]
 Hence Proved.

Note: The construction was too important. Without it we cannot determine if the angles are equal or not. And we know that if 2 tangents are drawn from a single point to the same circle the sides are equal and clearly PAB is an isosceles triangle so from there we can also say that the adjacent angles will be equal.