Question

Prove that the tangent drawn at the midpoint of an arc of a circle is parallel to the chord joining the end points of the arc.

Answer 1

Hint: Here we take an arc that has a mid-point through which the tangent of the circle passes. We join the end points of the arc and mid-point of the arc to the center of the circle to form two triangles. Using the SAS congruence rule we show both triangles congruent to each other. Use the property of tangents of a circle that states the radius makes a right angle with tangent at the point of contact. We show the interior angles between the tangent and chord to be \[{90^ \circ }\].

Complete step-by-step answer:
We draw a circle with center O. Draw an arc AB having mid-point N through which the tangent of the circle passes. Join OA, OB and ON.

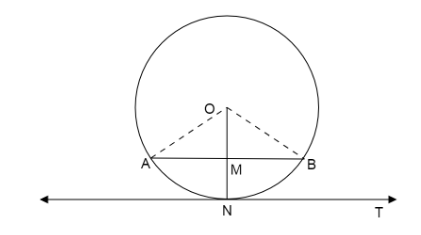
We know that tangent meets the radius of the circle at right angles.
\[ \Rightarrow \angle ONT = {90^ \circ }\] … (1)
Since, N is the mid-point of the arc AB, then point P divides the arc into two equal halves i.e. AN and NB.
We know equal arcs subtend equal angles at the center.
\[ \Rightarrow \angle AON = \angle BON\]
Therefore, we can say
\[ \Rightarrow \angle AOM = \angle BOM\] … (2)
Now in \[\vartriangle AOM\]and\[\vartriangle BOM\]
\[AO = BO\](Radii of the same circle)
\[\angle AOM = \angle BOM\](From equation (2))
\[OM = OM\](Common side)
Then we can say by SAS congruence rule\[\vartriangle AOM \cong \vartriangle BOM\]
We know if any two triangles are congruent then their corresponding angles are equal.
\[ \Rightarrow \angle AMO = \angle BMO\]
Now we know angles lying on a straight line are supplementary in nature.
So, the sum of angles \[\angle AMO,\angle BMO\]is equal to \[{180^ \circ }\]
\[ \Rightarrow \angle AMO + \angle BMO = {180^ \circ }\]
Substitute the value of \[\angle AMO = \angle BMO\]
\[ \Rightarrow \angle BMO + \angle BMO = {180^ \circ }\]
\[ \Rightarrow 2\angle BMO = {180^ \circ }\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{2\angle BMO}}{2} = \dfrac{{{{180}^ \circ }}}{2}\]
Cancel the same terms from numerator and denominator on both sides of the equation.
\[ \Rightarrow \angle BMO = {90^ \circ }\] … (3)
NOW, from equations (1) and (3) \[\angle ONT = {90^ \circ }\]and\[\angle BMO = {90^ \circ }\]
\[ \Rightarrow \angle BMO = \angle ONT\]
Also,\[\angle BMO\] is corresponding angle to \[\angle ONT\]and are equal in measure.
We know that when parallel lines are cut by a transversal they make equal corresponding angles.
Therefore, the tangent NT is parallel to chord AB.

Note: * SAS congruence rule states that two triangles are said to be congruent to each other if two sides and the included angle of one triangle is equal to the two sides and the including angle of the other triangle.
* Radius of a triangle makes a right angle with the tangent of the circle at the point of contact.
Also, keep in mind supplementary angles are always on a straight line and give sum \[{180^ \circ }\].