Question

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Answer 1

Hint: A Rhombus is a flat shape with 4 equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal.
Also diagonals of a rhombus bisect each other at a right angle.
So we can apply Pythagoras theorem for the right angled triangle formed by the half of the diagonals with one side of the rhombus. Then we can derive from that, the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals by putting the equal sides of the Rhombus in the equation.

Complete step-by-step answer:
Let, \[ABCD\] is a rhombus with diagonals \[AC\] and \[BD\] intersecting at \[O\].

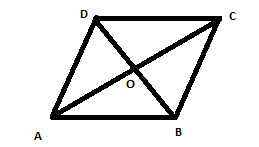
We need to prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
That is, \[A{B^2} + B{C^2} + C{D^2} + D{A^2} = A{C^2} + B{D^2}\].
Since \[ABCD\] is a rhombus, the sides of \[ABCD\] are equal.
Thus we get, .
We know that diagonals of a rhombus bisect each other at a right angle.
Then we get, \[\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ \].
Also,
\[ \Rightarrow AO = OC = \dfrac{1}{2}AC.....(1)\]
\[ \Rightarrow BO = OD = \dfrac{1}{2}BD....(2)\]
Now \[AOB\] is a right angle triangle.
We can apply Pythagoras theorem for the right angled \[\Delta AOB\],
We get,
\[ \Rightarrow A{B^2} = A{O^2} + O{B^2}\]
Using (1) and (2) we get,
\[ \Rightarrow A{B^2} = {\left( {\dfrac{1}{2}AC} \right)^2} + {\left( {\dfrac{1}{2}BD} \right)^2}\]
Taking square on both sides,
\[ \Rightarrow A{B^2} = \dfrac{1}{4}A{C^2} + \dfrac{1}{4}B{D^2}\]
Simplifying the terms we get,
\[ \Rightarrow A{B^2} = \dfrac{{A{C^2} + B{D^2}}}{4}\]
Solving it for get the required result,
\[ \Rightarrow 4A{B^2} = A{C^2} + B{D^2}\]
\[ \Rightarrow A{B^2} + A{B^2} + A{B^2} + A{B^2} = A{C^2} + B{D^2}\]
Since the sides of the Rhombus are equal.
\[ \Rightarrow A{B^2} + B{C^2} + C{A^2} + D{A^2} = A{C^2} + B{D^2}\]
Hence, the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Note: You will get a rectangle, where the midpoints of the 4 sides are joined together, and the length and width of the rectangle will be half the value of the main diagonal so that the area of the rectangle will be half of the rhombus.
When the shorter diagonal is equal to one of the sides of a rhombus, two congruent equilateral triangles are formed.
Pythagoras theorem states that,
If \[ABC\] is a right angled triangle then,
\[{{\text{(Hypotenuse)}}^{\text{2}}}{\text{ = (Height}}{{\text{)}}^{\text{2}}}{\text{ + (Base}}{{\text{)}}^{\text{2}}}\]
\[A{C^2} = A{B^2} + B{C^2}\]