Question

Prove that the slope of a non-vertical line passing through the points A \[\left( {{x}_{1}},{{y}_{1}} \right)\] and B \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[m=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\].

Answer 1

Hint: To prove \[m=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\] first of all we will have to consider the two points on the Cartesian plane (x-y) and then join the points to each other and construct a right angle triangle with the distance between the points as a hypotenuse. We know that the slope of a line is equal to the tangent value of angle made by the line and x-axis in anticlockwise direction.
Complete step-by-step answer:
Let us consider the given points A \[\left( {{x}_{1}},{{y}_{1}} \right)\] and B \[\left( {{x}_{2}},{{y}_{2}} \right)\] in the x-y plane and the angle made by the line with x-axis in anticlockwise direction to be \['\theta '\].

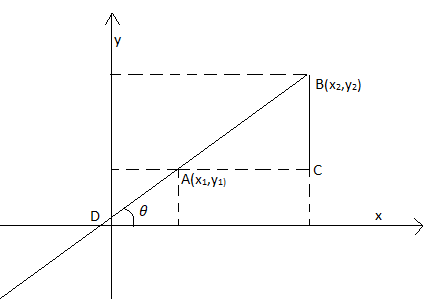
Since AC is parallel to x-axis and BD cuts them, we can say that,
\[\Rightarrow \angle BAC=\theta \] as these are corresponding angles
From the figure, we can get AC and BC by subtracting the corresponding x and y coordinates of points A, B and C. A and C have the same coordinates.
\[AC={{x}_{2}}-{{x}_{1}}\] and \[BC={{y}_{2}}-{{y}_{1}}\]
Now in triangle \[\Delta ABC\], we have as follows:
\[\tan A=\dfrac{BC}{AC}\]
Since \[\angle A=\theta \], \[AC={{x}_{2}}-{{x}_{1}}\] and \[BC={{y}_{2}}-{{y}_{1}}\]
\[\Rightarrow \tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
Since we know that slope of a line (m) is also equal to the tangent value of angle made by the line with x-axis in anticlockwise direction.
\[\Rightarrow slope(m)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\tan \theta \]
Therefore, it is proved that the slope of a line passing through A \[\left( {{x}_{1}},{{y}_{1}} \right)\] and B \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].

Note: Remember that if the slope of a line is equal to zero then it is parallel to x-axis and if the slope tends to infinity then it is perpendicular to x-axis. Also, you can remember that if the x-coordinates of the two points through which line passes are same then it must be perpendicular to x-axis and if y-coordinates of the two points through which line passes are same then it must be perpendicular to y-axis or parallel to x-axis.