Question

Prove that the segments joining the points of contact of a two parallel tangent passes through the centre.

Answer 1

Hint: In this question, we need to draw the diagram clearly in order to understand the relation between the angles. Then by using the properties of parallel lines having a transversal we can get the relation between the angles and prove that the segments joining the points of contact of two parallel tangents passes through the centre.

Complete step-by-step answer:
Let us look at some of the basic definitions.

LINE: Any line segment when extended indefinitely in both the directions is called line.

LINE SEGMENT: A part of a line with two endpoints is called a line segment.

PARALLEL LINES: When a straight line XY cuts two parallel lines l and m, then the line XY is called the transversal line. The following are the relationships between various angles that are formed.

Alternate angles are equal.

Corresponding angles are equal.

Sum of interior angles on the same side of the transversal line is equal to \[{{180}^{\circ }}\].
 Sum of exterior angles on the same side of the transversal line is equal to \[{{180}^{\circ }}\].
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.

TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior.

 Two circles are said to touch each other, if a common tangent can be drawn touching both the circles at the same point. This is called the point of contact.

Now, let us draw a diagram from the above given conditions.

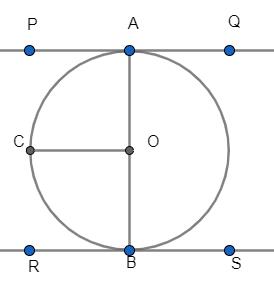
We need to prove that AOB is a straight line passing through O.

Let PAQ and RBS be two parallel tangents to a circle with centre O.

Now, let us join OA and OB and draw

\[OC\parallel PQ\]

Now, we have

\[PA\parallel CO\]

As we already know that sum of the angles on the same side of a transversal is \[{{180}^{\circ }}\]

\[\Rightarrow \angle PAO+\angle COA={{180}^{\circ }}\]

We already know that tangent drawn at a point is perpendicular to the radius at that point.

\[\begin{align}
  & \Rightarrow {{90}^{\circ }}+\angle COA={{180}^{\circ }} \\
 & \Rightarrow \angle COA={{90}^{\circ }} \\
\end{align}\]

Similarly,

\[\Rightarrow \angle RBO+\angle COB={{180}^{\circ }}\]

\[\Rightarrow {{90}^{\circ }}+\angle COB={{180}^{\circ }}\]

\[\Rightarrow \angle COB={{90}^{\circ }}\]

\[\Rightarrow \angle COA+\angle COB={{180}^{\circ }}\]

Hence, AOB is a straight line passing through the centre.

Note: It is important to note that the sum of the interior angles on the same side of the transversal line is equal to \[{{180}^{\circ }}\]. Because it is one of the important points to establish the relation between the angles which on further simplification shows that AOB is a straight line as it makes an angle of \[{{180}^{\circ }}\].
In the above question neglecting any of the conditions like parallel lines, angles that are on the same side of the transversal line, tangent drawn at a point is perpendicular to the radius at the point may not give us the result required to prove.