Question

Prove that the ratio of two areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

Answer 1

Hint:Consider two triangles say $\vartriangle DEF{\text{ and }}\vartriangle {\text{MNK}}$, which are similar by SSS property, use the postulate of SSS congruence that if two triangles are similar then the ratio of their respective sides are same as well.Considering two triangles as right angled triangle then find ratio of area of two triangles and substitute value of ratio of their respective sides and prove it.

Complete step-by-step answer:
We have to prove
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = {\left( {\dfrac{{DE}}{{MN}}} \right)^2}$
Proof –
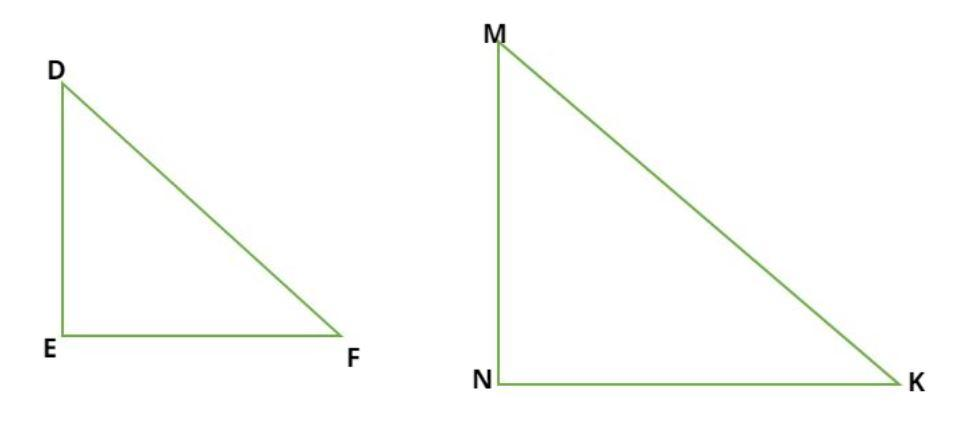
Consider the similar triangles DEF and MNK as shown in figure.
By the property of similar triangles, if two triangles are similar then the ratio of their respective sides are same i.e. (SSS congruence)
$ \Rightarrow \dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}} = \dfrac{{FD}}{{KM}}$............................. (a)
Now, we consider both as right angle triangle
So, the area of the right angle triangle is half multiplied by base time’s perpendicular.
$\begin{gathered}
   \Rightarrow A\left( {\Delta DEF} \right) = \dfrac{1}{2}\left( {EF} \right)\left( {DE} \right).............\left( 1 \right) \\
   \Rightarrow A\left( {\Delta MNK} \right) = \dfrac{1}{2}\left( {NK} \right)\left( {MN} \right).............\left( 2 \right) \\
\end{gathered} $
So, divide equation (1) from equation (2)
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = \dfrac{{\dfrac{1}{2}\left( {EF} \right)\left( {DE} \right)}}{{\dfrac{1}{2}\left( {NK} \right)\left( {MN} \right)}} = \dfrac{{\left( {EF} \right)\left( {DE} \right)}}{{\left( {NK} \right)\left( {MN} \right)}}..........\left( 3 \right)$
Now from equation (a)
$\dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}}$
Therefore from equation (3)
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = \dfrac{{\left( {EF} \right)\left( {DE} \right)}}{{\left( {NK} \right)\left( {MN} \right)}} = {\left( {\dfrac{{DE}}{{MN}}} \right)^2}$
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = {\left( {\dfrac{{DE}}{{MN}}} \right)^2}$
So the ratio of the area of two similar triangles is equal to the square of their corresponding sides.
Hence proved.

Note – In general triangles can be proved congruent or similar using AAA, SSS, ASA or even AAS postulates, that is angle angle angle, side side side , angle side angle and angle angle side respectively. Once triangles are proved congruent then property of CPCT which is corresponding parts of congruent triangles, can be used to find relations between different sides of two triangles.