Question

Prove that the ratio of the areas of two similar triangles is equal to the square of the
Ratio of their corresponding medians.

Answer 1

Hint: -First you have to draw a diagram so that you can understand what has to be proved. Use the property of a similar triangle that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

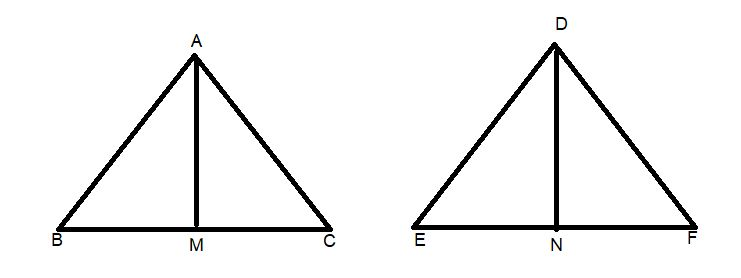
Complete step-by-step solution -
Given: -
Let $\Delta {\text{ABC}} \sim \Delta {\text{DEF}}$
Here AM is median
Hence BM=CM=$\dfrac{1}{2}{\text{BC}}$
Similarly, DN is median
Hence EN=FN=$\dfrac{1}{2}{\text{EF}}$
To prove: $\dfrac{{ar\left( {\Delta {\text{ABC}}} \right)}}{{ar\left( {\Delta {\text{DEF}}} \right)}} = \dfrac{{{\text{A}}{{\text{M}}^2}}}{{{\text{D}}{{\text{N}}^2}}}$
Proof:$\Delta {\text{ABC}} \sim \Delta {\text{DEF}}$$\left( {given} \right)$
The property of similar triangle ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
$\therefore \dfrac{{ar\left( {\Delta {\text{ABC}}} \right)}}{{ar\left( {\Delta {\text{DEF}}} \right)}} = \dfrac{{{\text{A}}{{\text{B}}^2}}}{{{\text{D}}{{\text{E}}^2}}} \ldots \left( 1 \right)$
It is also a property of similar triangles that corresponding sides of similar triangles are in the same proportion.
So, $\dfrac{{{\text{AB}}}}{{{\text{DE}}}} = \dfrac{{{\text{BC}}}}{{{\text{EF}}}} = \dfrac{{{\text{CA}}}}{{{\text{FD}}}} \ldots \left( 2 \right)$
$ \Rightarrow \dfrac{{{\text{AB}}}}{{{\text{DE}}}} = \dfrac{{\dfrac{1}{2}{\text{BC}}}}{{\dfrac{1}{2}{\text{EF}}}} = \dfrac{{{\text{BM}}}}{{{\text{EN}}}}$$ \ldots \ldots \left( 3 \right)$
In $\Delta {\text{ABM}}$and $\Delta {\text{DEN}}$, we have
$\angle B = \angle E\left[ {\because \Delta {\text{ABC}} \sim \Delta {\text{DEF}}} \right]$(corresponding angle of similar triangle are equal)
$\dfrac{{{\text{AB}}}}{{{\text{DE}}}} = \dfrac{{{\text{BM}}}}{{{\text{EN}}}}\left[ {{\text{proved in }}\left( 3 \right)} \right]$
$\therefore \Delta {\text{ABM}} \sim \Delta {\text{DEN by SAS similarity criterian}}{\text{.}}$
$\therefore \dfrac{{{\text{AB}}}}{{{\text{DE}}}} = \dfrac{{{\text{AM}}}}{{{\text{DN}}}}$$ \ldots \ldots \left( 4 \right)$ (corresponding sides of similar triangle are proportional)
We know the ratio areas of two similar triangles are equal to the squares of the corresponding sides.
$\therefore \dfrac{{ar\left( {\Delta {\text{ABC}}} \right)}}{{ar\left( {\Delta {\text{DEF}}} \right)}} = \dfrac{{{\text{A}}{{\text{B}}^2}}}{{{\text{D}}{{\text{E}}^2}}} = \dfrac{{{\text{A}}{{\text{M}}^2}}}{{{\text{D}}{{\text{N}}^2}}}$ (using equation 4 $\left( {\dfrac{{{\text{AB}}}}{{{\text{DE}}}} = \dfrac{{{\text{AM}}}}{{{\text{DN}}}}} \right)$)
Hence proved.

Note: -The key concept of solving is first draw a diagram and write what is given and what has to be proved. Then use the properties of a similar triangle to prove the question. You should have remembered all the properties.