Question

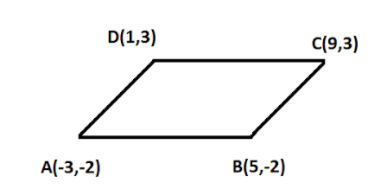
Prove that the points, \[A( - 3, - 2),B(5, - 2),C(9,3),D(1,3)\] are the vertices of a parallelogram.

Answer 1

Hint: Here we are given 4 points. To prove that it is a parallelogram, we need to calculate the length of the sides, we use the distance formula for it. And then check if opposite sides are equal.

Complete step-by-step answer:
We know that the distance between the two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is,
\[d = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\]
Let the given vertices be \[A = \left( { - 3, - 2} \right),\;B = \left( {5, - 2} \right),\;C = (9,3)\] and \[D = \left( {1,3} \right)\]

 We first find the distance between \[A = \left( { - 3, - 2} \right)\;\]and \[B = \left( {5, - 2} \right)\;\;\]as follows:
 \[AB = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\]​
On substituting the values of \[A = \left( { - 3, - 2} \right)\;\]and \[B = \left( {5, - 2} \right)\;\;\], we get,
\[ = \sqrt {{{\left( {5 - ( - 3)} \right)}^2} + {{\left( {( - 2) - ( - 2)} \right)}^2}} \;\]
On simplifying we get,
\[ = \sqrt {{{\left( {8} \right)}^2} + {{\left( {0} \right)}^2}} \;\]
\[ = \sqrt {64} \]
On taking positive root we get,
\[ = 8\]units
 Similarly, the distance between \[B = \left( {5, - 2} \right)\;\]and \[C = \left( {9,3} \right)\;\] is:
 \[BC = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\]
On substituting the values of \[B = \left( {5, - 2} \right)\;\]and \[C = \left( {9,3} \right)\;\], we get,
\[ = \sqrt {{{\left( {9 - 5} \right)}^2} + {{\left( {3 - ( - 2)} \right)}^2}} \;\]
On simplifying we get,
\[ = \sqrt {{{\left( 4 \right)}^2} + {{\left( {5} \right)}^2}} \;\]
\[ = \sqrt {16 + 25} \;\]
\[ = \sqrt {41} \;\]units
 Now, the distance between \[C = \left( {9,3} \right)\;\] and \[D = (1,3)\;\]is:
\[CD = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\]
On substituting the value of \[C = \left( {9,3} \right)\;\] and \[D = (1,3)\;\], we get,
\[ = \sqrt {{{\left( {1 - 9} \right)}^2} + {{\left( {3 - 3} \right)}^2}} \;\]
On further simplification we get,
\[ = \sqrt {{{\left( { - 8} \right)}^2} + {{\left( 0 \right)}^2}} \;\]
\[ = \sqrt {64} \;\]
On taking positive square root we get,
\[ = 8\]units
 Now, the distance between \[D = \left( {1,3} \right)\;\]and \[A = \left( { - 3, - 2} \right)\;\] is:
 \[DA = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\]
On substituting the values of \[D = \left( {1,3} \right)\;\]and \[A = \left( { - 3, - 2} \right)\;\], we get,
\[ = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( { - 2 - 3} \right)}^2}} \;\]
On simplifying further we get,
\[ = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 5} \right)}^2}} \;\]
\[ = \sqrt {16 + 25} \;\]
\[ = \sqrt {41} \]units
 We also know that if the opposite sides have equal side lengths, then ABCD is a parallelogram.
Here, since the lengths of the opposite sides are equal that is:
\[AB = CD = 8\]units and \[BC = DA = \sqrt {41} \]units.
Hence, the given vertices are the vertices of a parallelogram.

Note: There are also other important properties of parallelograms to know:
1.Opposite sides are congruent \[\left( {AB{\text{ }} = {\text{ }}DC} \right).\]
2.Opposite angles are congruent \[\left( {D{\text{ }} = {\text{ }}B} \right).\]
3.Consecutive angles are supplementary \[\left( {A{\text{ }} + {\text{ }}D{\text{ }} = {\text{ }}180^\circ } \right).\]
4.If one angle is right, then all angles are right.
5.The diagonals of a parallelogram bisect each other.
6.Each diagonal of a parallelogram separates it into two congruent triangles.