Question

Prove that the perimeter of a triangle is greater than the sum of its three medians.

Answer 1

Hint: In this question we will use the inequality property of a triangle to prove the given statement.

Complete Step-by-Step solution:
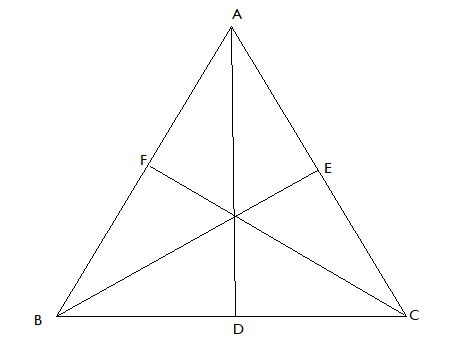
Now, the median is the line drawn from vertex to its opposite side, which divides the side in two equal parts. In the given question ABC is a triangle and AD, BE, CF are medians drawn from vertex A, B, C respectively which divides the opposite side in two equal parts. Now, as AD is median to side BC, then BD = DC. Similarly, BE and CF are medians to side AC and AB respectively, therefore AE = EC and AF = FB.
Now, we will use an inequality property of the triangle which states that the sum of any two sides of a triangle is greater than twice the median with respect to the third side. We will use this property to prove the given statement.
Now, the perimeter of a triangle is equal to the sum of all three sides of the triangle. So, the given statement is
AB + BC + AC > AD + BE + CF
We have to prove the above statement.
Now, from the figure, in triangle ABC, applying the inequality of triangle stated above, we get
 AB + AC > 2AD …… (1)
Also, in triangle ABC applying the inequality, we get
AB + BC > 2BE …… (2)
Again, in triangle ABC, we get
AC + BC > 2CF …… (3)
Adding equations (1), (2) and (3), we get
2 (AB + BC + AC) > 2 (AD + BE + CF)

Therefore, AB + BC + AC > AD + BE + CF
Hence proved.

Note: To solve such types of questions, it is recommended that students should follow some steps to solve the given problem. First, read the questions carefully and go through the figure given in the question. After it, write the mathematical form of the statement to be proved. Then, apply the property related to the question to solve the given problem. Students generally got confused because they don’t write what they have to prove and they got no idea where to start and they got stuck. So, it is very important that we write what we have to prove and also apply proper properties to solve the question.