Question

Prove that the normal chord of a parabola ${{y}^{2}}=4ax$ at the point $\left( p,p \right)$ subtends at a right angle at the focus.

Answer 1

Hint: The normal chord of a parabola ${{y}^{2}}=4ax$ at a point $\left( p,p \right)$ that means whose ordinate is equal to abscissa. If $\left( a{{t}^{2}},2at \right)$ be any point the parabola ${{y}^{2}}=4ax$, then $a{{t}^{2}}=2at$.

Complete step-by-step answer:
The given equation of the parabola is ${{y}^{2}}=4ax$ when the ordinate is equal to abscissa.

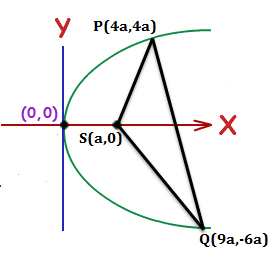
Let $P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$be any point on the parabola ${{y}^{2}}=4ax$, then
Focus of the parabola is S(a,0)
$a{{t}_{1}}^{2}=2a{{t}_{1}}$
Dividing both sides by $a{{t}_{1}}$, we get
${{t}_{1}}=2$
So, the coordinates of the point P are $\left( 4a,4a \right)$.
Let us assume that PQ is a normal chord and normal at the point P to the parabola ${{y}^{2}}=4ax$.
Let the coordinates of the point$Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$, then
${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}=-2-\dfrac{2}{2}=-3$
So, the coordinates of the point Q are$\left( 9a,-6a \right)$.
Therefore, the slope of SP= $\dfrac{4a-0}{4a-a}=\dfrac{4a}{3a}=\dfrac{4}{3}$ and the slope of SQ = $\dfrac{-6a-0}{9a-a}=\dfrac{-6a}{8a}=\dfrac{-3}{4}$
Now, the slope of SP $\times $ Slope of SQ = $\dfrac{4}{3}\times \dfrac{-3}{4}=-1$
Since the product of slopes of two straight lines is equal to -1, then these two lines are perpendicular.
Hence, the normal chord makes a right angle at the focus.
Note: If the normal at the point $P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ meets the parabola ${{y}^{2}}=4ax$ again at the point $Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$, then ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$. PQ is normal to the parabola at the point P and not at the point Q.