Question

Prove that the locus of the mid-point of chords of the parabola ${y^2} = 4ax$ which touches the parabola ${y^2} = 4bx$ is${y^2}\left( {2a - b} \right) = 4{a^2}x$.

Answer 1

Hint: Midpoint of chord touches another parabola its mean that the chord will be a tangent to the parabola, so consider chord a tangent to${y^2} = 4bx$ parabola. Consider the points on parabola in the form of$(a{t^2},2at)$ .

Complete step-by-step answer:
Let the given parabola ${y^2} = 4ax$ has a chord, which cuts parabola at $(a{t_1}^2,2a{t_1})$& $(a{t_2}^2,2a{t_2})$ .

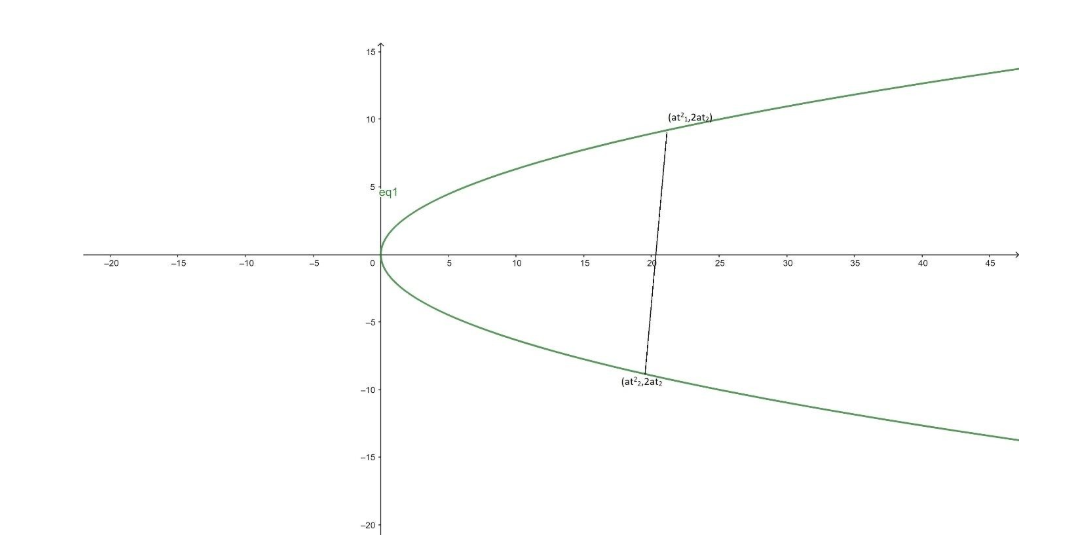
Let the given midpoint of chord AB be$\left( {h,k} \right)$ .
We know midpoint of a line joining two point $\left( {x,y} \right)\& \left( {m,n} \right)$ =$\left( {\dfrac{{x + m}}{2},\dfrac{{y + n}}{2}} \right)$ .
$h = \left( {\dfrac{{a{t^2}_1 + a{t^2}_2}}{2}} \right)$ & $k = \left( {\dfrac{{2a{t_1} + 2a{t_2}}}{2}} \right)$
$h = \dfrac{a}{2}\left( {{t^2}_1 + {t^2}_2} \right)$ …(1)
& $k = a\left( {{t_1} + {t_2}} \right)$ …(2)
Now,
$2h = a\left( {{t^2}_1 + {t^2}_2} \right)$
Now manipulating it as ${(a + b)^2} = {a^2} + {b^2} + 2ab$ ,
$2h = a{\left( {({t_1} + {t_2}} \right)^2} - 2{t_1}{t_2})$
From equation (2).
..
${t_1}{t_2} = \dfrac{{{k^2}}}{{2{a^2}}} - \dfrac{h}{a}$ …(3)
Now find the equation of chord passing through two points at $(a{t_1}^2,2a{t_1})$& $(a{t_2}^2,2a{t_2})$ .
Using two point formula of equation of line $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_1} - {x_1}}}\left( {x - {x_1}} \right)$ .
Then,
$y - 2a{t_1} = \dfrac{{\left( {2a{t_2} - 2a{t_1}} \right)}}{{a{t^2}_2 - a{t^2}_1}}\left( {x - a{t^2}_1} \right)$
Taking a common from numerator and denominator & then expand denominator.$\left( {{a^2} - {b^2}} \right) = \left( {a - b} \right)\left( {a + b} \right)$ .
$
  y - 2a{t_1} = \dfrac{{2\left( {{t_2} - {t_1}} \right)}}{{{t^2}_2 - {t^2}_1}}\left( {x - a{t^2}_1} \right) \\
  y - 2a{t_1} = \dfrac{{2\left( {{t_2} - {t_1}} \right)}}{{({t_2} + {t_1})\left( {{t_2} - {t_1}} \right)}}\left( {x - a{t^2}_1} \right) \\
  y - 2a{t_1} = \dfrac{2}{{({t_2} + {t_1})}}\left( {x - a{t^2}_1} \right) \\
  (y - 2a{t_1})({t_2} + {t_1}) = 2\left( {x - a{t^2}_1} \right) \\
  y({t_2} + {t_1}) - 2a{t_1}{t_2} - 2a{t^2}_1 = 2x - 2a{t^2}_1 \\
$
$ - 2a{t^2}_1$ will be cancel out from both side
Then, we get
$
  y({t_2} + {t_1}) - 2a{t_1}{t_2} = 2x \\
    \\
$
Equation of chord will be
$y=\dfrac{2x}{{({t_2}+{t_1})}} + \dfrac{{2a{t_1}{t_2}}}{{({t_2} + {t_1})}}$ …(4)
Now in the question it is said that the locus of the mid points of chords of the parabola touches the parabola ${y^2} = 4bx$ .
We know if a chord touches a parabola at a point only, then it must be a tangent to the parabola.
Condition for a line of slope m : $y = mx + c$ to be a tangent to parabola ${y^2} = 4bx$ is $c = \dfrac{b}{m}$ .

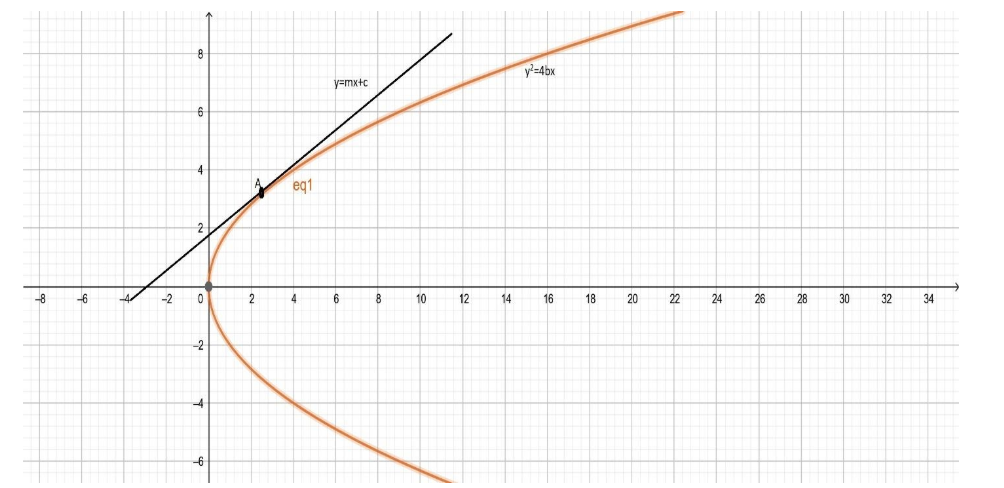
From equation (4)
$m = \dfrac{2}{{({t_2} + {t_1})}}$ & $c = \dfrac{{2{a_{{t_1}}}{t_2}}}{{\left( {{t_1} + {t_2}} \right)}}$
Now according to the condition stated.
$c = \dfrac{b}{m}$
$\dfrac{{2a{t_1}{t_2}}}{{\left( {{t_1} + {t_2}} \right)}} = \dfrac{{b({t_2} + {t_1})}}{2}$
$4a{t_1}{t_2} = b({\left( {{t_1} + {t_2}} \right)^2}$
Now using equation (2) &(3).
$4a\left( {\dfrac{{{k^2}}}{{2{a^2}}} - \dfrac{h}{a}} \right) = b\left( {\dfrac{{{k^2}}}{{{a^2}}}} \right)$
Now manipulating the equation to get desired answer,
$\begin{gathered}
  4a\left( {\dfrac{{{k^2} - 2ah}}{{2{a^2}}}} \right) = \dfrac{{b{k^2}}}{{{a^2}}} \\
  2a{k^2} - 4{a^2}h = b{k^2} \\
  {k^2}(2a - b) = 4{a^2}h \\
\end{gathered} $
Now replace $(h,k)$ with $(x,y)$
Then,
${y^2}(2a - b) = 4{a^2}x$
Hence, it’s proved that the locus of the midpoint of chords of the parabola ${y^2} = 4ax$ which touches the parabola ${y^2} = 4bx$ is${y^2}\left( {2a - b} \right) = 4{a^2}x$.

Note: Equation of a tangent to a parabola passing through point $(h,k)$ can be given as $yk = 2a(x + h)$ which can be directly used to solve it.