Question

Prove that the locus of a point, which moves so that its distance from a fixed line is equal to the length of the tangent drawn from it to a given circle, is a parabola. Find the position of the focus and directrix.

Answer 1

Hint: First of all, we need to take the given condition on the co-ordinate plane and then take the given line to be parallel to the y – axis and the given circle to have center at (0, 0) and then find the locus of point.

Complete step-by-step answer:
Let the given circle have a center O which is the origin and radius r and the given line is AB.

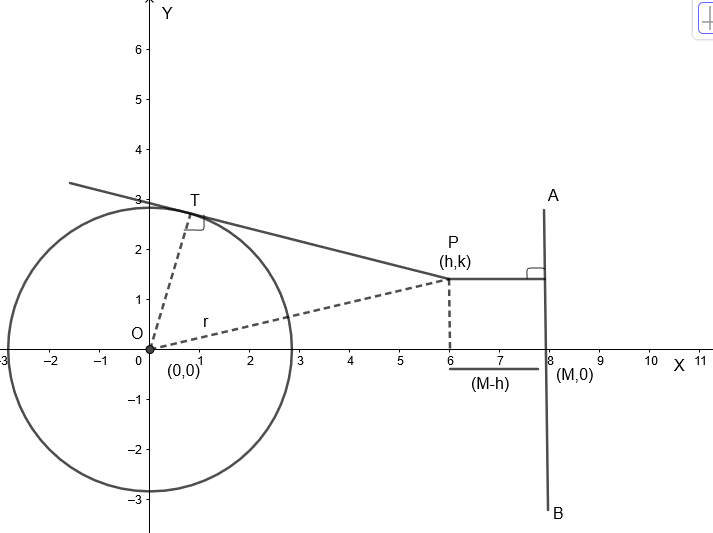
From the figure, we get, given circle is \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}:{{C}_{1}}\]
And the given line is x = M, also OT = r = radius. Also, the point P whose locus to be found be (h, k).
By Pythagoras theorem, \[O{{T}^{2}}+T{{P}^{2}}=P{{O}^{2}}\]
Therefore, length of tangent \[TP=\sqrt{P{{O}^{2}}-O{{T}^{2}}}=\sqrt{P{{O}^{2}}-{{r}^{2}}}\]
By distance formula, \[OP=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}{{h}^{2}}}=\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}\]
Therefore, we get \[TP=\sqrt{{{h}^{2}}+{{k}^{2}}-{{r}^{2}}}.....\left( i \right)\]
Also, distance of point P(h, k) from given line = (M – h)…..(ii) by diagram
By equating equations (i) and (ii), we get,
\[\sqrt{{{h}^{2}}+{{k}^{2}}-{{r}^{2}}}=\left( M-h \right)\]
Squaring both sides,
\[{{\left( x-y \right)}^{2}}={{x}^{2}}+{{y}^{2}}-2xy\]
Also, \[{{h}^{2}}+{{k}^{2}}-{{r}^{2}}={{M}^{2}}+{{h}^{2}}-2Mh\]
\[{{k}^{2}}=-2Mh+{{M}^{2}}+{{r}^{2}}\]
\[\Rightarrow {{k}^{2}}=-2M\left( h-\dfrac{\left( {{M}^{2}}+{{r}^{2}} \right)}{2M} \right)\]
Replacing k by y and h by x to get the locus.
\[{{y}^{2}}=-2M\left[ h-\dfrac{\left( {{M}^{2}}+{{r}^{2}} \right)}{2M} \right]\]
which is of the form of parabola \[{{y}^{2}}=4a\left( x-h \right)\]
which has focus \[=\left\{ \left( h+a \right),0 \right\}\]

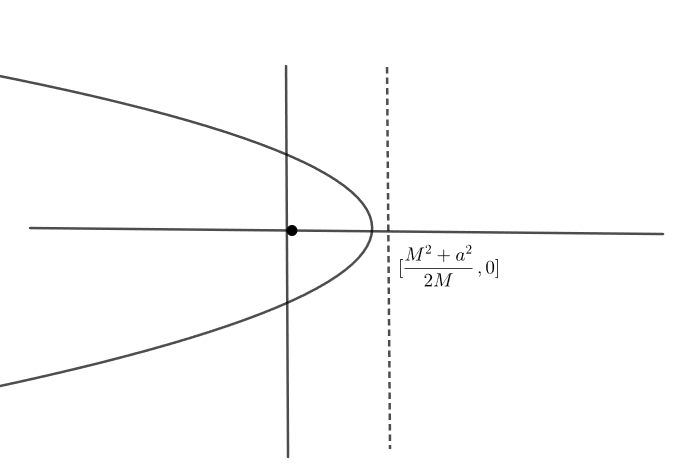
\[=\left\{ \left( \dfrac{{{M}^{2}}+{{r}^{2}}}{2M}-\dfrac{M}{2} \right),0 \right\}\]
\[=\left\{ \dfrac{{{r}^{2}}}{2M},0 \right\}\]
And directrix is X = h – a
\[X=\dfrac{{{M}^{2}}+{{r}^{2}}}{2M}+\dfrac{M}{2}\]
Rearranging the equation, we get \[2Mx=2{{M}^{2}}+{{r}^{2}}\].

Note: Students should be careful when doing these types of questions. We need to take the origin as the center as questions can get lengthy and confusing if any other arbitrary point is taken. Students often get confused in formulas for negative focus but it is the same as the general formula.