Question

Prove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.

Answer 1

Hint: We will use the congruent parts of congruent triangles in which if any two angles are congruent to each other then their corresponding sides and angles will also be equal.

Complete step-by-step answer:
First we will draw a circle with A as its centre point. Then we will draw any two chords in the circle wherever we want to draw. A chord is not radius but a shorter line which is drawn at the arc of a circle. The chords have been represented by ED and CB in the figure below. Now, we will convert these lines into triangles shown as $\Delta ABC$ and $\Delta ADE$. After that two mid-points are drawn equally bisecting the chords denoted by AG on CB and AF on ED. As we know that the bisectors separates the line into two equal parts. Therefore, we have that the chords BC and ED are bisected equally resulting in CG = GB and FD = FE.
The diagram for the question is given below.

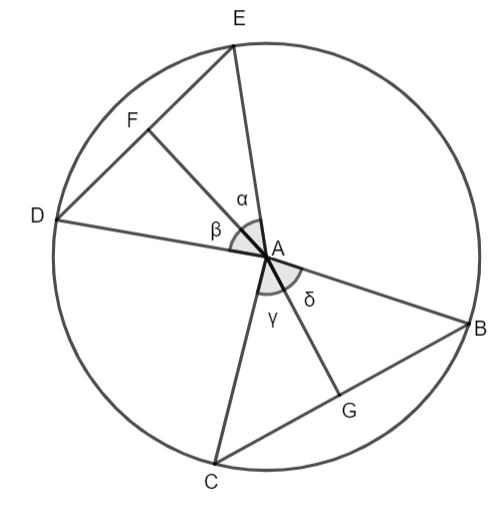
Now, we will first prove that $\Delta ABC$ and $\Delta ADE$ are congruent to each other. As we can clearly see that in the diagram we have AD, AE, AC and AB are the radius or radii of the circle. (The plural of radius is written as radii). So, they all will be equal to each other. Therefore, we have
AE = AB
AD = AC
Now, as we have drawn two equal chords on the guidance of the question thus, we have that BC = ED. Clearly, by the side-side-side theorem in which if the all three sides, of two triangles are equal then they are also congruent. Thus, we have that $\Delta ABC\cong ~\Delta ADE$.
Now, we will apply the congruent parts of congruent triangles in which if any two angles are congruent to each other then their corresponding sides and angles will also be equal. Therefore, we have that $\angle BAC=\angle EAD$.
Hence, the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.

Note: Forming the diagram stepwise will make the diagram correct. The radius is never equal to the chord of a circle. We also have got additional information that $\angle EAF=\angle FAD$ and similarly, $\angle BAG=\angle GAC$.