Question

Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed, is $6\sqrt {3r} $

Answer 1

Hint: In order to prove this question we will use the property that tangents on a circle are equal from an external point and perimeter of a triangle is the sum of all three sides of it. Use these properties to prove the question.

Complete step-by-step answer:
Referring from diagram

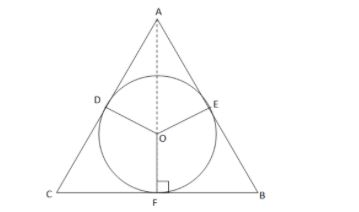
Let ABC be isosceles is \[AB = AC = x\] ,
“r” is radius of circle and BC= y and a circle with centre O and radius r is inscribed in the triangle. Join OA and OE and OD.
Sides AB, AC and BC are the tangents to the circle.
As the radius makes a right angle with the tangent to the circle at the point of intersection. So, triangle AFB is right angled at F.
In right angle triangle ABF, we will apply Pythagoras theorem
$
   \Rightarrow {\left( {AF} \right)^2} + {\left( {BF} \right)^2} = {\left( {AB} \right)^2} \\
   \Rightarrow {\left( {3r} \right)^2} + {\left( {\dfrac{y}{2}} \right)^2} = {\left( x \right)^2}...........{\text{(1) }}\left[ {\because BF = \dfrac{{BC}}{2}} \right] \\
 $
Now again from triangle ADO, we will apply Pythagoras theorem
$
   \Rightarrow {\left( {AD} \right)^2} + {\left( {DO} \right)^2} = {\left( {AO} \right)^2} \\
   \Rightarrow {\left( {AD} \right)^2} + {\left( r \right)^2} = {\left( {2r} \right)^2} \\
 $
(OA= 2r because center of the circle divides altitude of the triangle in the ratio 2:1)
$
   \Rightarrow {\left( {AD} \right)^2} + {r^2} = 4{r^2} \\
   \Rightarrow {\left( {AD} \right)^2} = 4{r^2} - {r^2} \\
   \Rightarrow {\left( {AD} \right)^2} = 3{r^2} \\
   \Rightarrow AD = \sqrt {3{r^2}} \\
   \Rightarrow AD = \sqrt 3 r \\
 $
Now, BE = BF and AD = AE (Since tangents drawn from an external point are equal) ---(2)
​So,
$
  AB = BE + AE \\
  x = BE + AE \\
  x = BF + AD{\text{ }}\left[ {{\text{from equation (2)}}} \right] \\
   \Rightarrow x = \sqrt 3 r + \dfrac{y}{2} \\
   \Rightarrow \dfrac{y}{2} = x - \sqrt 3 r..........(3) \\
$
Putting value of equation (3) in equation (1), we get
\[
  \because {\left( {3r} \right)^2} + {\left( {\dfrac{y}{2}} \right)^2} = {\left( x \right)^2} \\
   \Rightarrow {\left( {3r} \right)^2} + {\left( {x - \sqrt 3 r} \right)^2} = {\left( x \right)^2} \\
   \Rightarrow 9{r^2} + {x^2} - 2\sqrt 3 rx + 3{r^2} = {\left( x \right)^2} \\
   \Rightarrow 12{r^2} - 2\sqrt 3 rx = 0 \\
   \Rightarrow 12{r^2} = 2\sqrt 3 rx \\
   \Rightarrow 6r = \sqrt 3 x \\
   \Rightarrow x = \dfrac{{6r}}{{\sqrt 3 }} \\
 \]
Put the value of x in equation (3), we have
$
  \because \dfrac{y}{2} = x - \sqrt 3 r \\
   \Rightarrow \dfrac{y}{2} = \dfrac{{6r}}{{\sqrt 3 }} - \sqrt 3 r \\
   \Rightarrow \dfrac{y}{2} = \dfrac{{6\sqrt 3 r}}{3} - \sqrt 3 r \\
   \Rightarrow \dfrac{y}{2} = \dfrac{{6\sqrt 3 r - 3\sqrt 3 r}}{3} \\
   \Rightarrow \dfrac{y}{2} = \dfrac{{3\sqrt 3 r}}{3} \\
   \Rightarrow y = 2\sqrt 3 r \\
 $
So we get the sides of triangle \[AB = AC = x = \dfrac{{6r}}{{\sqrt 3 }}\] and \[BC = y = 2\sqrt 3 r\]
As we know that the perimeter of a triangle is equal to the sum of all the sides.
Therefore, perimeter of triangle ABC = 2AB + BC
\[
   = 2x + y \\
   = 2 \times \left( {\dfrac{{6r}}{{\sqrt 3 }}} \right) + 2\sqrt 3 r \\
   = \dfrac{{12r}}{{\sqrt 3 }} + 2\sqrt 3 r \\
   = \dfrac{{12r + 6r}}{{\sqrt 3 }} \\
   = \dfrac{{18r}}{{\sqrt 3 }} \\
   = \dfrac{{18r}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} \\
   = \dfrac{{18\sqrt 3 r}}{3} \\
   = 6\sqrt 3 r \\
 \]
So, the perimeter is $6\sqrt {3r} $
Hence, the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed, is $6\sqrt {3r} $

Note: The sides of the isosceles triangle inscribing the circle are the tangent to the circle. Also tangents drawn from an external point are equal. In order to solve such problems students must remember the different properties of tangent to the circle. Some of them are mentioned in the solution. Students must draw figures for solving such questions.