Question

Prove that the lateral surface area of the cube is $4{{a}^{2}}$.

Answer 1

Hint: To specify a figure most fundamental quantities are perimeter, area and volume for a three-dimensional object. Area can be defined as the space occupied by a flat shape or the surface of an object. So, using this definition, we can easily prove the desired part in our problem.

Complete step-by-step answer:


According to our problem, we are given a cube having side length as a. We have to prove that the lateral surface area of the cube is $4{{a}^{2}}$.
For proving this, we must know what is meant by lateral surface area. There are two types of surface area related to a solid. One is the total surface area and other is the lateral surface area. Total surface area includes the area of all the surfaces while the lateral surface area includes the area excluding the top and bottom surfaces.
Therefore, a cube has four lateral surfaces after excluding the top and bottom surfaces. Area of one lateral surface is the area of a square, that is ${{a}^{2}}$. The below given cube shows the lateral surface area excluding the top and bottom surfaces.

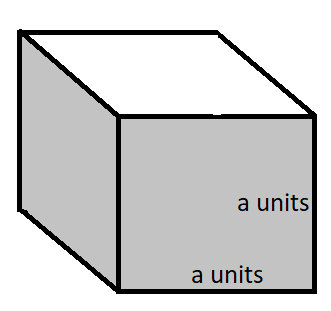
The lateral surface area of cube $=4{{a}^{2}}$.
Hence, we prove that the lateral surface area of the cube is $4{{a}^{2}}$.

Note: The key concept involved in solving this problem is the knowledge of surface area of three dimensional solid particularly lateral surface area. By using that simple definition of lateral surface area, we proved our result.