Question

Prove that the function f given by $f(x) = x - \left[ x \right]$ is increasing on $(0,1)$.

Answer 1

Hint: First we will learn about the greatest integer function using that we’ll find the value of the function $f(x)$. Then we will differentiate the function with-respect-to x to find the derivative of the function to find whether the function is increasing or not in the interval $(0,1)$

Complete step by step answer:

Given data: $f(x) = x - \left[ x \right]$
We know that $\left[ x \right]$ is the greatest integer function where it gives an integer value lesser or equal to ‘x’.
Now, we have given the domain for the function $f(x)$ i.e. $(0,1)$
From the definition of the greatest integer function, we can say that in the interval $(0,1)$
$ \Rightarrow \left[ x \right] = 0$
Hence, where $x \in (0,1)$
So we have $f(x) = x - 0$
\[ \Rightarrow f(x) = x\]
On differentiating with-respect-to x, we get,
$ \Rightarrow f'(x) = 1$ and $1 > 0$
Now, we know that if the derivative of a function is always positive in $(a,b)$, then it is increasing in$(a,b)$
similarly if the derivative of a function is always negative $(c,d)$, the function will be decreasing in the interval$(c,d)$.
Therefore we can say that the function is increasing in $(0,1)$

Note: We can also that the function f is increasing in $(0,1)$ by plotting the graph of the function in the interval of $(0,1)$

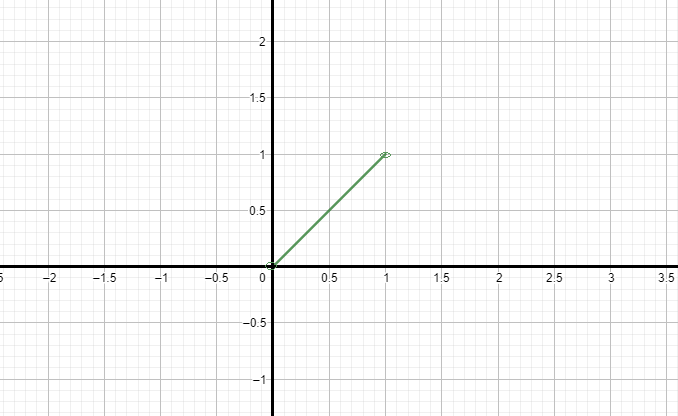
In the graph also we can see that the function is increasing in the interval $(0,1)$.