
Prove that the equation to the circle, which passes through the focus and touches the parabola ${{y}^{2}}=4ax$ at the point $(a{{t}^{2}},2at)$, is
${{x}^{2}}+{{y}^{2}}-ax(3{{t}^{2}}+1)-ay(3t-{{t}^{3}})+3{{a}^{2}}{{t}^{2}}=0$.
Prove also that the locus of its centre is the curve
$27a{{y}^{2}}=(2x-a){{(x-5a)}^{2}}$.
Answer
596.7k+ views
Hint: Assume a general equation of the circle, and then substitute for the values of the $x$ and $y$ coordinates of the centre, and the constant term, by making the points which it passes through satisfy the equation. Next, find a relation between the $x$ and $y$ coordinates of the centre by eliminating $t$ from the equations.
Complete step-by-step answer:
Let the equation of the circle we want to find out be : ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\text{ }\left( 1 \right)$
Here is a better understanding of what the figure would look like :
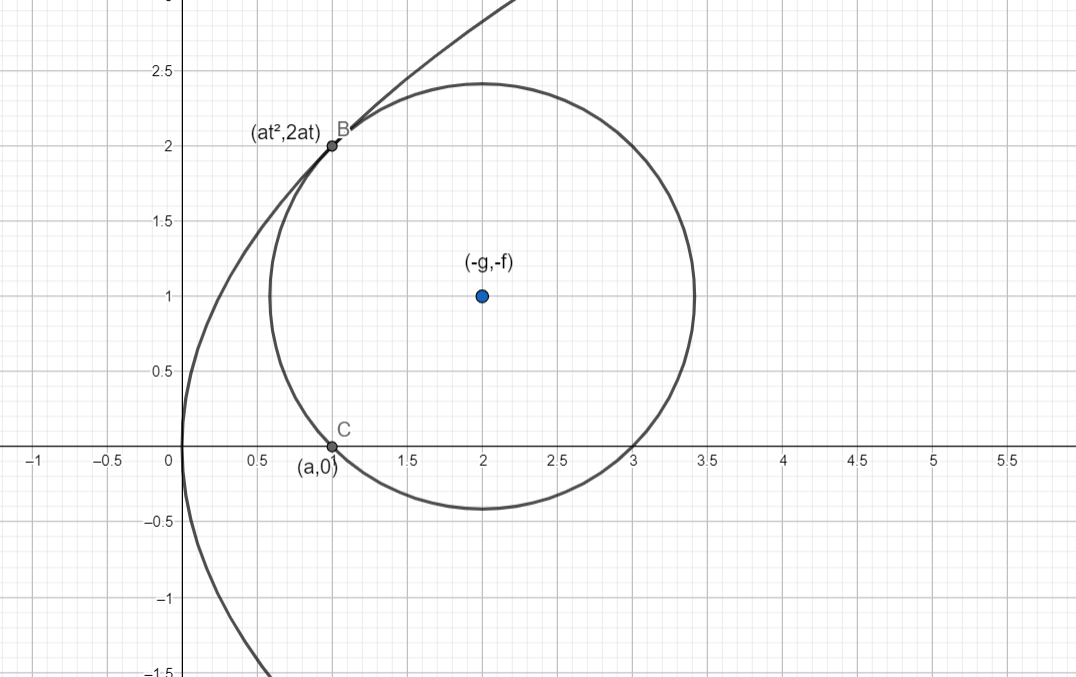
As you can see here, the circle touches the parabola at the focus, as well as the general point mentioned.
For the parabola ${{P}_{1}}:{{y}^{2}}=4ax$, we know that its vertex is at $(0,0)$and its focus is at $(a,0)$. Since the conditions mentioned in the question is that the focus of the parabola lies on the circle, the first thing we’re going to do is satisfy equation (1) of the circle we want, with the point $(a,0)$.
Substituting $x=a$ and $y=0$, we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& \Rightarrow {{a}^{2}}+0+2ga+2f0+c=0 \\
& \Rightarrow {{a}^{2}}+2ag+c=0 \\
& \Rightarrow c=-2ag-{{a}^{2}} \\
\end{align}$
Thus, we have expressed $c$ in terms of $g$ and $a$. Let’s substitute this value in equation (1) to simplify it into a lesser number of variables. Doing so, we get
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0\text{ }\left( 2 \right) \\
\end{align}$
The next step would be further simplification of (2) to find an equation that does not have the variables $g$ and $f$. An easy method to do that would be by finding the tangent at the point $(a{{t}^{2}},2at)$. Since this point lies on a parabola, we can use the formula of a general tangent to a parabola ${{y}^{2}}=4ax$, having a slope $m$. The general formula of the tangent to a parabola ${{y}^{2}}=4ax$ is :
$y=mx+\dfrac{a}{m}\text{ }\left( 3 \right)$
Equation (3) is the equation of the tangent to the parabola at the point $(a{{t}^{2}},2at)$. Therefore, $(a{{t}^{2}},2at)$ should satisfy equation (3). Substituting, we get :
$\begin{align}
& y=mx+\dfrac{a}{m} \\
& \Rightarrow 2at=ma{{t}^{2}}+\dfrac{a}{m} \\
\end{align}$
Dividing both sides by $a$, we get :
$\begin{align}
& \Rightarrow 2t=m{{t}^{2}}+\dfrac{1}{m} \\
& \Rightarrow 2t=\dfrac{{{m}^{2}}{{t}^{2}}+1}{m} \\
& \Rightarrow 2mt={{m}^{2}}{{t}^{2}}+1 \\
& \Rightarrow {{m}^{2}}{{t}^{2}}-2mt+1=0 \\
& \Rightarrow {{(mt-1)}^{2}}=0 \\
& \Rightarrow mt-1=0 \\
& \Rightarrow mt=1 \\
& \Rightarrow m=\dfrac{1}{t} \\
\end{align}$
Since equation (3) should pass through the point $(a{{t}^{2}},2at)$, and act as a tangent to the circle and parabola both, we can now say that the line joining the circle’s centre to the point $(a{{t}^{2}},2at)$ will be perpendicular to this tangent. This is because the radius of a circle is perpendicular to any tangent drawn at the same point that the radius ends on the circle.
Therefore, the product of the slope of the line joining the centre of the circle, $(-g,-f)$ and the point $(a{{t}^{2}},2at)$, and the slope of the tangent, will be $-1$.
Written mathematically, it means :
$(\dfrac{2at-(-f)}{a{{t}^{2}}-(-g)})m=-1$
Substituting for $m$, in terms of $t$, we get :
$\begin{align}
& (\dfrac{2at+f}{a{{t}^{2}}+g})(\dfrac{1}{t})=-1 \\
& \Rightarrow 2at+f=-t(a{{t}^{2}}+g) \\
& \Rightarrow 2at+f=-a{{t}^{3}}-gt \\
& \Rightarrow f=-a{{t}^{3}}-gt-2at \\
\end{align}$
Thus, we have successfully expressed $f$ in terms of $a,g$ and $t$. This leaves us with only one variable to eliminate, $g$.
To eliminate $g$, we should make the point $(a{{t}^{2}},2at)$ satisfy the equation (2). This is because, after all, the circle does pass through $(a{{t}^{2}},2at)$ since it touches the parabola at that very point. Making point $(a{{t}^{2}},2at)$ satisfy equation (2), we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{(a{{t}^{2}})}^{2}}+{{(2at)}^{2}}+2ga{{t}^{2}}+2f(2at)-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g+4atf-2ag-{{a}^{2}}=0 \\
\end{align}$
Now, we’ll substitute for $f$, using the expression we got expressing $f$ in terms of $g,a$ and $t$.
Doing so, we get :
$\begin{align}
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g+4at(-a{{t}^{3}}-gt-2at)-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g-4{{a}^{2}}{{t}^{4}}-4ag{{t}^{2}}-8{{a}^{2}}{{t}^{2}}-2ag-{{a}^{2}}=0 \\
& \Rightarrow -3{{a}^{2}}{{t}^{4}}-4{{a}^{2}}{{t}^{2}}-2ag{{t}^{2}}-2ag-{{a}^{2}}=0 \\
& \Rightarrow 2ag{{t}^{2}}+2ag=-3{{a}^{2}}{{t}^{4}}-4{{a}^{2}}{{t}^{2}}-{{a}^{2}} \\
& \Rightarrow 2ag({{t}^{2}}+1)=-{{a}^{2}}(3{{t}^{4}}+4{{t}^{2}}+1) \\
& \Rightarrow 2g=\dfrac{-{{a}^{2}}(3{{t}^{4}}+3{{t}^{2}}+{{t}^{2}}+1)}{a({{t}^{2}}+1)} \\
& \Rightarrow 2g=\dfrac{-a(3{{t}^{2}}+1)({{t}^{2}}+1)}{({{t}^{2}}+1)} \\
& \Rightarrow 2g=-a(3{{t}^{2}}+1) \\
\end{align}$
Thus, we have successfully even expressed $g$ in terms of $a$ and $t$.
Next, we need to substitute the value of $g$ in the expression where we found $f$ in terms of $g,a$ and $t$.
Doing so, we get :
$\begin{align}
& f=-a{{t}^{3}}-gt-2at \\
& \Rightarrow 2f=-2a{{t}^{3}}-2gt-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}-t(-a(3{{t}^{2}}+1))-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}+at(3{{t}^{2}}+1)-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}+3a{{t}^{3}}+at-4at \\
& \Rightarrow 2f=a{{t}^{3}}-3at \\
& \Rightarrow 2f=-a(3t-{{t}^{3}}) \\
\end{align}$
And hence, we have even successfully expressed $f$ in terms of $a$ and $t$.
Substituting the values of $2g$ and $2f$ with what we obtained, in equation (2), we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y-a(-a(3{{t}^{2}}+1))-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+{{a}^{2}}(3{{t}^{2}}+1)-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+3{{a}^{2}}{{t}^{2}}+{{a}^{2}}-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+3{{a}^{2}}{{t}^{2}}=0 \\
\end{align}$
Hence, we have arrived at the equation of the circle required.
The next part of the question asks us to find the locus of the centre of this very circle. From equation (1), we can derive that the centre of the circle = $(-g,-f)$.
All we need to do now is find a relation between $g$ and $f$, that does not contain the term $t$. So our goal is to eliminate $t$ from the relations we got for $g$ and $f$, expressing them in terms of $a$ and $t$.
For $g$, the equation we have is : $2g=-a(3{{t}^{2}}+1)\text{ }\left( 4 \right)$
For $f$, the equation we have is : $2f=-a(3t-{{t}^{3}})\text{ }\left( 5 \right)$
Let's find the point whose locus we need to find as $(h,k)$. Since this point is the same as the circle’s centre, we can say that :
$\begin{align}
& h=-g\,\,\,\text{ and }\,\,\,\,\,k=-f \\
& \Rightarrow g=-h\text{ and }f=-k \\
\end{align}$
Substituting for $g$ and $f$ in (4) and (5) respectively, we have :
From equation (4), we get
$\begin{align}
& 2f=-a(3t-{{t}^{3}}) \\
& \Rightarrow 2f=-at(3-{{t}^{2}}) \\
& \Rightarrow -2k=at({{t}^{2}}-3) \\
& \Rightarrow -\dfrac{2k}{at}={{t}^{2}}-3 \\
& \Rightarrow -\dfrac{2k}{at}+3={{t}^{2}} \\
\end{align}$
From equation (5), we get
$\begin{align}
& 2g=-a(3{{t}^{2}}+1) \\
& \Rightarrow 2g=-3a{{t}^{2}}-a \\
& \Rightarrow -2h=-3a{{t}^{2}}-a \\
& \Rightarrow 2h=3a{{t}^{2}}+a \\
& \Rightarrow 2h-a=3a{{t}^{2}} \\
& \Rightarrow \dfrac{2h-a}{3a}={{t}^{2}} \\
\end{align}$
We now have equations expressing ${{t}^{2}}$ in terms of both, $h$ and $k$.
Equating these two expressions, we get :
$\begin{align}
& -\dfrac{2k}{at}+3=\dfrac{2h-a}{3a} \\
& \Rightarrow \dfrac{-2k+3at}{at}=\dfrac{2h-a}{3a} \\
& \Rightarrow \dfrac{-2k+3at}{t}=\dfrac{2h-a}{3} \\
& \Rightarrow (-2k+3at)3=t(2h-a) \\
& \Rightarrow -6k+9at=2ht-at \\
& \Rightarrow 10at-2ht=6k \\
& \Rightarrow 5at-ht=3k \\
& \Rightarrow t(5a-h)=3k \\
& \Rightarrow t=\dfrac{3k}{5a-h} \\
\end{align}$
Thus, we finally have a value of $t$ only in terms of $h$ and $k$.
Substituting this value of $t$ in equation (3), along with the substituted value of $g$, we get :
$\begin{align}
& 2g=-a(3{{t}^{2}}+1) \\
& \Rightarrow -\dfrac{2g}{a}=3{{t}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3{{t}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3{{(\dfrac{3k}{5a-h})}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3(\dfrac{9{{k}^{2}}}{{{(5a-h)}^{2}}})+1 \\
& \Rightarrow \dfrac{2h}{a}=\dfrac{27{{k}^{2}}+{{(5a-h)}^{2}}}{{{(5a-h)}^{2}}} \\
& \Rightarrow 2h{{(5a-h)}^{2}}=27a{{k}^{2}}+a{{(5a-h)}^{2}} \\
& \Rightarrow (2h-a){{(5a-h)}^{2}}=27a{{k}^{2}} \\
\end{align}$
Hence, we have obtained the locus of the centre of the circle. The last step in this sum would be to replace $(h,k)$ with $(x,y)$. Doing so, we get :
$\begin{align}
& 27a{{k}^{2}}=(2h-a){{(5a-h)}^{2}} \\
& \Rightarrow 27a{{y}^{2}}=(2x-a){{(5a-x)}^{2}} \\
\end{align}$
Hence, this equation is our required locus.
Hence proved, the given equation is the equation of the circle required, and the second equation is indeed the locus of the centre of the circle.
Note: When we are trying to find out the locus of some point, always first look at the equation given in the question and see which variable is missing. It means that we have to eliminate this very variable from the equations for $(h,k)$ or the point whose locus needs to be found out. Eventually, we will get a relation between $h$ and $k$ using the very equations you get while trying to eliminate the variable identified as not being present in the equation of the locus.
Complete step-by-step answer:
Let the equation of the circle we want to find out be : ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\text{ }\left( 1 \right)$
Here is a better understanding of what the figure would look like :

As you can see here, the circle touches the parabola at the focus, as well as the general point mentioned.
For the parabola ${{P}_{1}}:{{y}^{2}}=4ax$, we know that its vertex is at $(0,0)$and its focus is at $(a,0)$. Since the conditions mentioned in the question is that the focus of the parabola lies on the circle, the first thing we’re going to do is satisfy equation (1) of the circle we want, with the point $(a,0)$.
Substituting $x=a$ and $y=0$, we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& \Rightarrow {{a}^{2}}+0+2ga+2f0+c=0 \\
& \Rightarrow {{a}^{2}}+2ag+c=0 \\
& \Rightarrow c=-2ag-{{a}^{2}} \\
\end{align}$
Thus, we have expressed $c$ in terms of $g$ and $a$. Let’s substitute this value in equation (1) to simplify it into a lesser number of variables. Doing so, we get
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0\text{ }\left( 2 \right) \\
\end{align}$
The next step would be further simplification of (2) to find an equation that does not have the variables $g$ and $f$. An easy method to do that would be by finding the tangent at the point $(a{{t}^{2}},2at)$. Since this point lies on a parabola, we can use the formula of a general tangent to a parabola ${{y}^{2}}=4ax$, having a slope $m$. The general formula of the tangent to a parabola ${{y}^{2}}=4ax$ is :
$y=mx+\dfrac{a}{m}\text{ }\left( 3 \right)$
Equation (3) is the equation of the tangent to the parabola at the point $(a{{t}^{2}},2at)$. Therefore, $(a{{t}^{2}},2at)$ should satisfy equation (3). Substituting, we get :
$\begin{align}
& y=mx+\dfrac{a}{m} \\
& \Rightarrow 2at=ma{{t}^{2}}+\dfrac{a}{m} \\
\end{align}$
Dividing both sides by $a$, we get :
$\begin{align}
& \Rightarrow 2t=m{{t}^{2}}+\dfrac{1}{m} \\
& \Rightarrow 2t=\dfrac{{{m}^{2}}{{t}^{2}}+1}{m} \\
& \Rightarrow 2mt={{m}^{2}}{{t}^{2}}+1 \\
& \Rightarrow {{m}^{2}}{{t}^{2}}-2mt+1=0 \\
& \Rightarrow {{(mt-1)}^{2}}=0 \\
& \Rightarrow mt-1=0 \\
& \Rightarrow mt=1 \\
& \Rightarrow m=\dfrac{1}{t} \\
\end{align}$
Since equation (3) should pass through the point $(a{{t}^{2}},2at)$, and act as a tangent to the circle and parabola both, we can now say that the line joining the circle’s centre to the point $(a{{t}^{2}},2at)$ will be perpendicular to this tangent. This is because the radius of a circle is perpendicular to any tangent drawn at the same point that the radius ends on the circle.
Therefore, the product of the slope of the line joining the centre of the circle, $(-g,-f)$ and the point $(a{{t}^{2}},2at)$, and the slope of the tangent, will be $-1$.
Written mathematically, it means :
$(\dfrac{2at-(-f)}{a{{t}^{2}}-(-g)})m=-1$
Substituting for $m$, in terms of $t$, we get :
$\begin{align}
& (\dfrac{2at+f}{a{{t}^{2}}+g})(\dfrac{1}{t})=-1 \\
& \Rightarrow 2at+f=-t(a{{t}^{2}}+g) \\
& \Rightarrow 2at+f=-a{{t}^{3}}-gt \\
& \Rightarrow f=-a{{t}^{3}}-gt-2at \\
\end{align}$
Thus, we have successfully expressed $f$ in terms of $a,g$ and $t$. This leaves us with only one variable to eliminate, $g$.
To eliminate $g$, we should make the point $(a{{t}^{2}},2at)$ satisfy the equation (2). This is because, after all, the circle does pass through $(a{{t}^{2}},2at)$ since it touches the parabola at that very point. Making point $(a{{t}^{2}},2at)$ satisfy equation (2), we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{(a{{t}^{2}})}^{2}}+{{(2at)}^{2}}+2ga{{t}^{2}}+2f(2at)-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g+4atf-2ag-{{a}^{2}}=0 \\
\end{align}$
Now, we’ll substitute for $f$, using the expression we got expressing $f$ in terms of $g,a$ and $t$.
Doing so, we get :
$\begin{align}
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g+4at(-a{{t}^{3}}-gt-2at)-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{a}^{2}}{{t}^{4}}+4{{a}^{2}}{{t}^{2}}+2a{{t}^{2}}g-4{{a}^{2}}{{t}^{4}}-4ag{{t}^{2}}-8{{a}^{2}}{{t}^{2}}-2ag-{{a}^{2}}=0 \\
& \Rightarrow -3{{a}^{2}}{{t}^{4}}-4{{a}^{2}}{{t}^{2}}-2ag{{t}^{2}}-2ag-{{a}^{2}}=0 \\
& \Rightarrow 2ag{{t}^{2}}+2ag=-3{{a}^{2}}{{t}^{4}}-4{{a}^{2}}{{t}^{2}}-{{a}^{2}} \\
& \Rightarrow 2ag({{t}^{2}}+1)=-{{a}^{2}}(3{{t}^{4}}+4{{t}^{2}}+1) \\
& \Rightarrow 2g=\dfrac{-{{a}^{2}}(3{{t}^{4}}+3{{t}^{2}}+{{t}^{2}}+1)}{a({{t}^{2}}+1)} \\
& \Rightarrow 2g=\dfrac{-a(3{{t}^{2}}+1)({{t}^{2}}+1)}{({{t}^{2}}+1)} \\
& \Rightarrow 2g=-a(3{{t}^{2}}+1) \\
\end{align}$
Thus, we have successfully even expressed $g$ in terms of $a$ and $t$.
Next, we need to substitute the value of $g$ in the expression where we found $f$ in terms of $g,a$ and $t$.
Doing so, we get :
$\begin{align}
& f=-a{{t}^{3}}-gt-2at \\
& \Rightarrow 2f=-2a{{t}^{3}}-2gt-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}-t(-a(3{{t}^{2}}+1))-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}+at(3{{t}^{2}}+1)-4at \\
& \Rightarrow 2f=-2a{{t}^{3}}+3a{{t}^{3}}+at-4at \\
& \Rightarrow 2f=a{{t}^{3}}-3at \\
& \Rightarrow 2f=-a(3t-{{t}^{3}}) \\
\end{align}$
And hence, we have even successfully expressed $f$ in terms of $a$ and $t$.
Substituting the values of $2g$ and $2f$ with what we obtained, in equation (2), we get :
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy-2ag-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y-a(-a(3{{t}^{2}}+1))-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+{{a}^{2}}(3{{t}^{2}}+1)-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+3{{a}^{2}}{{t}^{2}}+{{a}^{2}}-{{a}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-a(3{{t}^{2}}+1)x-a(3t-{{t}^{3}})y+3{{a}^{2}}{{t}^{2}}=0 \\
\end{align}$
Hence, we have arrived at the equation of the circle required.
The next part of the question asks us to find the locus of the centre of this very circle. From equation (1), we can derive that the centre of the circle = $(-g,-f)$.
All we need to do now is find a relation between $g$ and $f$, that does not contain the term $t$. So our goal is to eliminate $t$ from the relations we got for $g$ and $f$, expressing them in terms of $a$ and $t$.
For $g$, the equation we have is : $2g=-a(3{{t}^{2}}+1)\text{ }\left( 4 \right)$
For $f$, the equation we have is : $2f=-a(3t-{{t}^{3}})\text{ }\left( 5 \right)$
Let's find the point whose locus we need to find as $(h,k)$. Since this point is the same as the circle’s centre, we can say that :
$\begin{align}
& h=-g\,\,\,\text{ and }\,\,\,\,\,k=-f \\
& \Rightarrow g=-h\text{ and }f=-k \\
\end{align}$
Substituting for $g$ and $f$ in (4) and (5) respectively, we have :
From equation (4), we get
$\begin{align}
& 2f=-a(3t-{{t}^{3}}) \\
& \Rightarrow 2f=-at(3-{{t}^{2}}) \\
& \Rightarrow -2k=at({{t}^{2}}-3) \\
& \Rightarrow -\dfrac{2k}{at}={{t}^{2}}-3 \\
& \Rightarrow -\dfrac{2k}{at}+3={{t}^{2}} \\
\end{align}$
From equation (5), we get
$\begin{align}
& 2g=-a(3{{t}^{2}}+1) \\
& \Rightarrow 2g=-3a{{t}^{2}}-a \\
& \Rightarrow -2h=-3a{{t}^{2}}-a \\
& \Rightarrow 2h=3a{{t}^{2}}+a \\
& \Rightarrow 2h-a=3a{{t}^{2}} \\
& \Rightarrow \dfrac{2h-a}{3a}={{t}^{2}} \\
\end{align}$
We now have equations expressing ${{t}^{2}}$ in terms of both, $h$ and $k$.
Equating these two expressions, we get :
$\begin{align}
& -\dfrac{2k}{at}+3=\dfrac{2h-a}{3a} \\
& \Rightarrow \dfrac{-2k+3at}{at}=\dfrac{2h-a}{3a} \\
& \Rightarrow \dfrac{-2k+3at}{t}=\dfrac{2h-a}{3} \\
& \Rightarrow (-2k+3at)3=t(2h-a) \\
& \Rightarrow -6k+9at=2ht-at \\
& \Rightarrow 10at-2ht=6k \\
& \Rightarrow 5at-ht=3k \\
& \Rightarrow t(5a-h)=3k \\
& \Rightarrow t=\dfrac{3k}{5a-h} \\
\end{align}$
Thus, we finally have a value of $t$ only in terms of $h$ and $k$.
Substituting this value of $t$ in equation (3), along with the substituted value of $g$, we get :
$\begin{align}
& 2g=-a(3{{t}^{2}}+1) \\
& \Rightarrow -\dfrac{2g}{a}=3{{t}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3{{t}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3{{(\dfrac{3k}{5a-h})}^{2}}+1 \\
& \Rightarrow \dfrac{2h}{a}=3(\dfrac{9{{k}^{2}}}{{{(5a-h)}^{2}}})+1 \\
& \Rightarrow \dfrac{2h}{a}=\dfrac{27{{k}^{2}}+{{(5a-h)}^{2}}}{{{(5a-h)}^{2}}} \\
& \Rightarrow 2h{{(5a-h)}^{2}}=27a{{k}^{2}}+a{{(5a-h)}^{2}} \\
& \Rightarrow (2h-a){{(5a-h)}^{2}}=27a{{k}^{2}} \\
\end{align}$
Hence, we have obtained the locus of the centre of the circle. The last step in this sum would be to replace $(h,k)$ with $(x,y)$. Doing so, we get :
$\begin{align}
& 27a{{k}^{2}}=(2h-a){{(5a-h)}^{2}} \\
& \Rightarrow 27a{{y}^{2}}=(2x-a){{(5a-x)}^{2}} \\
\end{align}$
Hence, this equation is our required locus.
Hence proved, the given equation is the equation of the circle required, and the second equation is indeed the locus of the centre of the circle.
Note: When we are trying to find out the locus of some point, always first look at the equation given in the question and see which variable is missing. It means that we have to eliminate this very variable from the equations for $(h,k)$ or the point whose locus needs to be found out. Eventually, we will get a relation between $h$ and $k$ using the very equations you get while trying to eliminate the variable identified as not being present in the equation of the locus.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




