Question

Prove that the diagonals of the rectangle ABCD, with vertices A (2,-1), B (5,-1), C (5, 6), D (2, 6) are equal & bisect each other.

Answer 1

Hint: Here we have to prove that both the diagonals of the rectangle are equal & bisect each other at some point.
At first we will show that both the diagonals are equal by the help of distance formula.
Distance formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
To show that both diagonals are bisecting each other, we have to show that both the triangles $\vartriangle AOB$ and $\vartriangle COD$ are congruent.
Definition of ASA test: Triangles are congruent if any two angles & their included side are equal in both the triangles.
CPCT theorem: The abbreviation of CPCT is corresponding parts of congruent triangles. This theorem states that if we consider two or more triangles which are congruent to each other then their corresponding angles and sides of the triangles are congruent to each other, equal to each other.

Complete step-by-step answer:
We have given rectangle ABCD, with vertices A (2,-1), B (5,-1), C (5, 6), D (2, 6).
For more clarity, Let us draw a diagram.

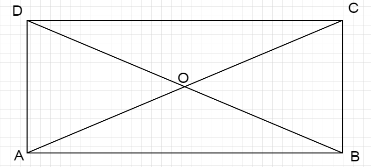
So, we have two diagonals AC & BD
1) In this step, we are showing that both diagonal are equal. For that, we have to find their lengths.
Let us find the length of diagonal AC by using distance formula.
We have A (2,-1), C (5, 6)
$\left( {{x_1},{y_1}} \right) = \left( {2, - 1} \right)$ & $\left( {{x_2},{y_2}} \right) = \left( {5,6} \right)$
Length of Diagonal AC $ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Substitute all values.
$ = \sqrt {{{\left( {5 - 2} \right)}^2} + {{\left( {6 - \left( { - 1} \right)} \right)}^2}} $
$ \Rightarrow \sqrt {{{\left( {5 - 2} \right)}^2} + {{\left( {6 + 1} \right)}^2}} $
Simplify it
$ \Rightarrow \sqrt {{{\left( 3 \right)}^2} + {{\left( 7 \right)}^2}} $
$ \Rightarrow \sqrt {9 + 49} $
$ \Rightarrow \sqrt {58} $ ……….1)
2) Length of diagonal BD $ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
We have B (5,-1), D (2, 6)
$\therefore \left( {{x_1},{y_1}} \right) = \left( {5, - 1} \right)$ & $\left( {{x_2},{y_2}} \right) = \left( {2,6} \right)$
Substitute all the values.
$ = \sqrt {{{\left( {2 - 5} \right)}^2} + {{\left( {6 - \left( { - 1} \right)} \right)}^2}} $
Simplify it
$ \Rightarrow \sqrt {{{\left( { - 3} \right)}^2} + {{\left( 7 \right)}^2}} $
$ \Rightarrow \sqrt {9 + 49} $
$ \Rightarrow \sqrt {58} $ …………2)
From 1) & 2) it is clear that diagonal AC & diagonal BD same value
$\therefore $ Both the diagonals are equal.
3) Now we have to show that both the triangles $\vartriangle AOB$ & $\vartriangle COD$ are congruent.
Both are the alternate interior angles of parallel lines.
$\therefore \angle OAB = \angle OCD$
Similarly, both are the alternate interior angles of parallel lines.
$\therefore \angle OBA = \angle ODC$
By the definition of the rectangle we can say that,
$AB = CD$
$\therefore $ By ASA test $\vartriangle AOB \cong \vartriangle COD$
4) By the corresponding parts of congruent triangles theorem we can say that,
$AO = CO$ & $BO = DO$
Hence, both the diagonals bisect each other at the point O.

Note: Students may confuse the distance formula.
In the distance formula, we did ${x_2} - {x_1}$ and ${y_2} - {y_1}$.
It is ok to use distance formula like ${x_1} - {x_2}$ and ${y_1} - {y_2}$
After these terms we did square. So it will be the same.