Question

How do you prove that the diagonals of a rectangle are congruent?

Answer 1

Hint: For proving that the diagonals of a rectangle are congruent. First of all we have to consider a rectangle and then we have to mark it as ABCD. By using SAS congruence rule, we can say that if one side and one angle of any triangles are congruent then the triangles are congruent. By this we can prove the diagonals of the rectangle are congruent.

Complete step by step answer:
From the given question we are given to prove that the diagonals of the rectangle are congruent. For that let us consider a rectangle named as ABCD with diagonals.

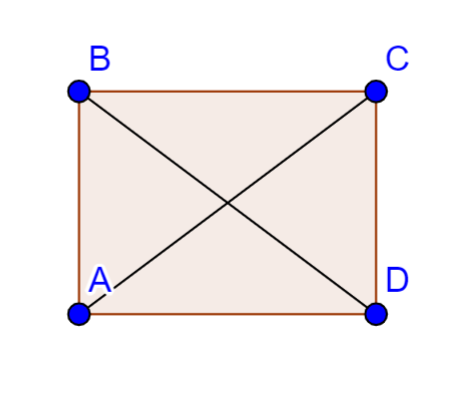
For showing that given diagonals are congruent I will consider two triangles in rectangle i.e. BAD and BCD.
So, here we have to prove
\[\text{Segment BD}\cong \text{ Segment AC}\]
As we know that every rectangle is a parallelogram, then it will satisfy the rule for a given rectangle also.
Let us consider two triangles ABC and BCD.
Now we have to prove that the sides AB and BC are congruent to CD and BC respectively, then we can automatically prove that the diagonals are congruent.
Since ABCD is a parallelogram, \[\text{Segment AB }\cong \text{ Segment DC}\]because opposite sides of a parallelogram are congruent.
\[\text{BC}\cong \text{BC}\] by the Reflexive Property of Congruence.
Furthermore, \[\angle BAD\] and \[\angle CDA\] are right angles by the definition of rectangle.
\[\angle BAD\cong \angle CDA\] since all right angles are congruent.
Now by solving the problem we can say that
\[\text{Segment AB }\cong \text{ Segment DC}\]
\[\text{BC}\cong \text{BC}\]
Therefore, by SAS, triangle \[ABC\text{ }\cong \text{ }\]triangle\[DCB\].
Since, by congruent rule if two triangles are congruent then their sides and angles are congruent.
Therefore, \[\text{Segment BD}\cong \text{ Segment AC}\].

Note:
We have some important things that you should be aware of about the proof above is the reflexive property that is always equal to itself. In order to prove that the diagonals of a rectangle are congruent, you could also use triangle ABD and triangle DCA.