Question

Prove that the diagonals of a parallelogram formed by the four-straight line $\sqrt{3}x+y=0,\sqrt{3}y+x=0,\sqrt{3}x+y=1,\sqrt{3}y+x=1$ are at right angles to one another.

Answer 1

Hint: For solving this problem, we first construct a parallelogram using the given equation and label the corresponding point of intersection. Then we will try to find the coordinates of points by solving the two equations of lines passing through that point, for x and y. Then we obtain the slope of both the diagonals and multiply them to check whether they are perpendicular or not.

Complete step-by-step answer:

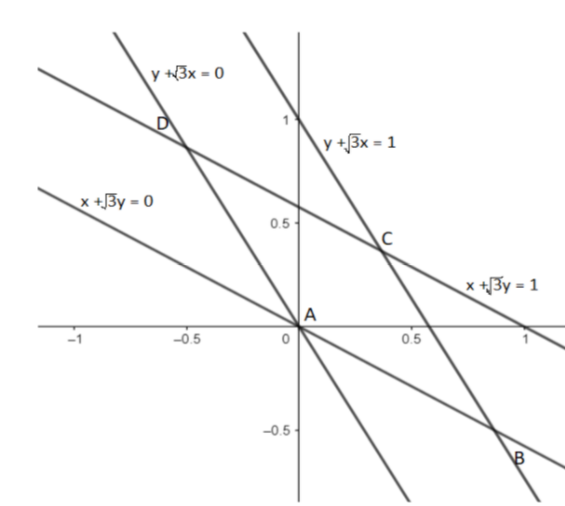
According to the question, we are given for equations:
$\begin{align}
  & \sqrt{3}y+x=0\ldots (1) \\
 & \sqrt{3}x+y=1\ldots (2) \\
 & \sqrt{3}y+x=1\ldots (3) \\
 & \sqrt{3}x+y=0\ldots (4) \\
\end{align}$
First considering equation (1) and (4) and solving for x and y to get the coordinates of A:
$\begin{align}
  & \sqrt{3}y+x=0\text{ and }\sqrt{3}x+y=0 \\
 & \therefore x=0,y=0 \\
\end{align}$
The coordinates of A are (0,0).
Now considering equation (1) and (2) and solving for x and y to get the coordinates of B:
$\sqrt{3}y+x=0\text{ and }\sqrt{3}x+y=1$
Now, multiplying equation (2) by $\sqrt{3}$ and then subtracting with equation (1), we get
$\begin{align}
  & \sqrt{3}\cdot \left( \sqrt{3}x+y \right)-\left( \sqrt{3}y+x \right)=\sqrt{3} \\
 & 3x-x+\sqrt{3}y-\sqrt{3}y=\sqrt{3} \\
 & x=\dfrac{\sqrt{3}}{2} \\
 & \therefore y=\dfrac{-1}{2} \\
\end{align}$
The coordinates of B are $\left( \dfrac{\sqrt{3}}{2},\dfrac{-1}{2} \right)$.
Now considering equation (2) and (3) and solving for x and y to get the coordinates of C:
$\sqrt{3}x+y=1\text{ and }\sqrt{3}y+x=1$
Now, multiplying equation (3) by $\sqrt{3}$ and then subtracting with equation (2), we get
$\begin{align}
  & \left( \sqrt{3}y+x \right)\cdot \sqrt{3}-\left( \sqrt{3}x+y \right)=\sqrt{3}-1 \\
 & 3y+\sqrt{3}x-\sqrt{3}x-y=\sqrt{3}-1 \\
 & y=\dfrac{\sqrt{3}-1}{2} \\
 & \therefore x=\dfrac{\sqrt{3}-1}{2} \\
\end{align}$
The coordinates of C are $\left( \dfrac{\sqrt{3}-1}{2},\dfrac{\sqrt{3}-1}{2} \right)$.
At last considering equation (3) and (4) and solving for x and y to get the coordinates of D:
$\sqrt{3}y+x=1\text{ and }\sqrt{3}x+y=0$
Now, multiplying equation (4) by $\sqrt{3}$ and then subtracting with equation (3), we get
\[\begin{align}
  & \left( \sqrt{3}x+y \right)\cdot \sqrt{3}-\left( \sqrt{3}y+x \right)=-1 \\
 & 3x+\sqrt{3}y-\sqrt{3}y-x=-1 \\
 & x=\dfrac{-1}{2} \\
 & \therefore y=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
The coordinates of D are \[\left( \dfrac{-1}{2},\dfrac{\sqrt{3}}{2} \right)\].
Now, by using the slope formula for two given points: $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{2}}}$
Slope of line formed by AC: ${{m}_{AC}}=\dfrac{\dfrac{\sqrt{3}-1}{2}-0}{\dfrac{\sqrt{3}-1}{2}-0}=1$
Slope of line formed by BD: ${{m}_{BD}}=\dfrac{\dfrac{\sqrt{3}}{2}-\left( \dfrac{-1}{2} \right)}{\dfrac{-1}{2}-\dfrac{\sqrt{3}}{2}}=-1$
So, on multiplying the slopes, we get
$\begin{align}
  & {{m}_{AC}}\times {{m}_{BD}}=1\times -1 \\
 & {{m}_{AC}}\times {{m}_{BD}}=-1 \\
\end{align}$
Hence, both of the lines are perpendicular.

Note: Whenever we are faced with such questions, first we have to draw a figure and then try to find the coordinates of the parallelogram. We have four straight lines, so intersection of two lines will give us the coordinates. Students must be careful while solving the equation of lines forming the parallelogram to obtain coordinates of corresponding points. We can name the coordinates first, then choose the respective lines and find (x, y). This will avoid any sort of confusion. Also, the slope must be calculated correctly for both the diagonals to obtain the desired result. We can also find the equation of lines AC and BD and then compute the slope from it if we don’t recollect the formula for slope.