Question

Prove that the diagonals of a parallelogram bisect each other.

Answer 1

Hint: We here have to prove that the diagonals of a parallelogram bisect each other. For this, we will first assume there to be a parallelogram ABCD whose diagonals will intersect each other at O. Then, we will see that as a result, 4 small triangles will be formed. Then we will consider any two opposite pairs of triangles and try to prove that they are congruent. Once they're proved to be congruent, the lines AO and OC will come out as equal and so will BO and OD as a result of CPCT rule. Hence, the diagonals will bisect each other.

Complete step by step answer:
We have to prove that the diagonals of a parallelogram bisect each other. For this, let us first assume there to be a ||gm ABCD whose diagonals AC and BD intersect each other at O.
This figure is given as follows:

Now, if we consider \[\Delta AOB\] and $\Delta COD$, we will see that:
Side AB=side CD as they both are opposite sides of the parallelogram and we know that opposite sides of parallelogram are equal.
We will also see that $\angle BAO=\angle DCO$ and $\angle ABO=\angle CDO$ as these are alternately opposite angles of the parallelogram and we know that the alternately opposite angles in a parallelogram are equal.
Thus, we can say that the triangles \[\Delta AOB\] and $\Delta COD$ are congruent by the rule of ASA (Angle Side Angle).
Hence, \[\Delta AOB\cong \Delta COD\]
Now, if we apply CPCT (Corresponding Parts of Congruent Triangles), we will be able to see that:
AO=OC
BO=OD
Now, we can see from the figure that:
AO+OC=AC
BO+OD=BD
Thus, we can say that O is the midpoint of lines AC and BD.

Hence, the diagonals bisect each other at O.

Note: We here could have taken any two opposite pair of triangles and also could have used any congruence criteria to prove them congruent. This is shown as follows:

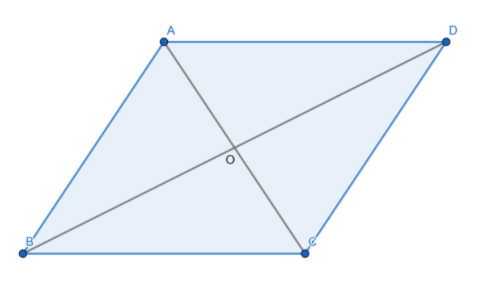
Let us consider $\Delta AOD$ and $\Delta COB$. In these triangles, we can see that:
$\angle AOD=\angle COB$ as they are vertically opposite angles
$\angle OAD=\angle OCB$ as they are alternately opposite angles
AD=BC as they are opposite sides of a parallelogram
Hence, $\Delta AOD\cong \Delta COB$