Question

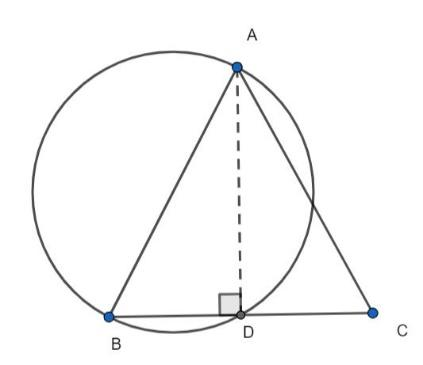
Prove that the circle drawn with any equal side of an isosceles triangle as diameter bisects the base.

Answer 1

Hint: Angle subtended by the diameter on any point of the circle is 90°. Then prove congruence between triangles ABD and ACD, then conclude that D bisects the base BC.

Complete step-by-step answer:
ABC is an isosceles triangle with AB and AC as equal sides and BC is the base of the triangle.
We are given that the circle drawn with any equal side, say AB, of an isosceles triangle, intersects the base at D. We need to prove that D bisects the base BC.

We know the property of the circle, where the angle subtended by the diameter of the circle or the semicircle on any point of the circle is equal to 90°.

Hence, the value of the angle ADB is equal to 90°.

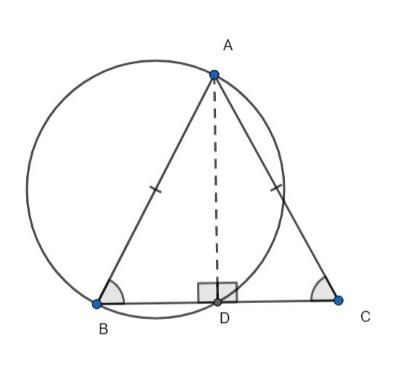
Consider the triangles ABD and ACD and check for congruency.

Both are right-angle triangles with right angles at D.

\[\angle ADB = \angle ADC = 90^\circ \] (Right-angle)

From the property of the isosceles triangle, the sides AB and AC are equal. AB and AC are also hypotenuse sides of the triangles ABD and ACD.

\[AB = AC\] (Hypotenuse)

The side AD is common to both the triangles ABD and ACD.

\[AD = AD\] (Side)

Hence, by Right-angle Hypotenuse Side (RHS) criterion, both the triangles are congruent to each other.

\[\Delta ABD \cong \Delta ACD\]

We know that the corresponding sides of the congruent triangle are equal. Hence, we have:
\[BD = CD\]

Hence, we conclude that D bisects the base BC.

Hence, the circle, drawn with any equal side of an isosceles triangle as diameter bisects the base.

Note: You can also prove congruence between the triangles by using any other criterion such as SAS or AAS. You can’t prove congruency using ASS, since it is not a sufficient condition.