Question

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

Answer 1

HINT: Before answering this question, let us know about the types of Triangles.
There are three types of triangles (according to the lengths of the sides):-
1. SCALENE TRIANGLE: A scalene triangle is a triangle having all the three sides of different lengths.
2. ISOSCELES TRIANGLE: An isosceles triangle is a triangle whose length of any two sides is equal.
3. EQUILATERAL TRIANGLE: An equilateral triangle is a triangle whose length of all the three sides is equal.
Also, we must know about the circle theorem.
From the Circle theorem we know that the angle inscribed on a semicircle is equal to 90°.

Complete step-by-step answer:

Let us consider an isosceles triangle ABC whose sides AB and AC are of equal length.

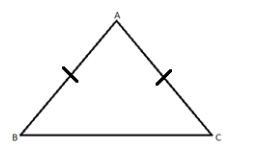
Now, let us take point ‘O’ in the middle of AB.

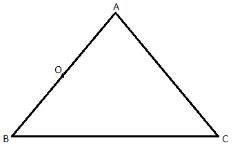
Now, let us construct a circle with center ‘O’ and radius equal to the length of AO. Also, let us take the point at, which the circle is cutting the line BC, to be ‘D’.

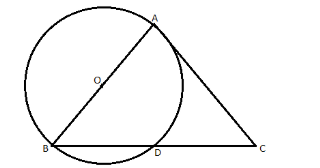
We will now draw a line AD, on BC.

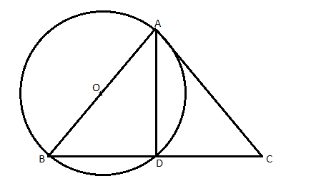
Now, as mentioned in the hint provided above, according to the circle theorem, an angle inscribed on a semicircle is always equal to 90°. Therefore, angle BDA is equal to 90°. And, as BDA is equal to 90°, therefore, ADC is also equal to 90°.

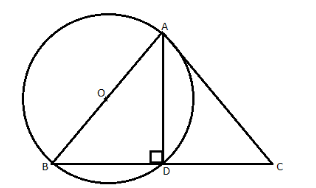
Now, as mentioned in the first step, AB = AC, so, now we will apply the RHS congruence criteria on the triangles ADB and ADC.
AB = AC (mentioned above)
AD = AD (common)
ADB = ADC = 90° (explained above)
So, BD = CD (CPCT)
As BD is equal to CD, therefore, the circle is bisecting BC.
Hence proved.

NOTE: Let us now learn about the classification of triangles on the basis of the measurement of their angles.
There are three types of triangles (according to the measurement of the angles):-
1. ACUTE – ANGLED TRIANGLE: An acute – angles triangle is a triangle whose measure of all the three angles is less than 90°.
2. OBTUSE – ANGLED TRIANGLE: An obtuse – angled triangle is a triangle whose measure of at least one angle is greater than 90°.
3. RIGHT – ANGLED TRIANGLE: A right – angled triangle is a triangle whose measure of at least one angle is equal to 90°.