Question

Prove that the bisectors of a pair of vertically opposite angles are in the same straight line.

Answer 1

Hint: Consider 2 pairs of lines that intersect at a point O. Bisect the angles that are formed at the point of intersection of both lines. As they are the bisectors, the angles are equal and the sum of all the angles formed at a point O is \[{{360}^{\circ }}\]. Thus prove that the bisectors form a straight line.

Complete step-by-step answer:

Let us assume that AB and CD are straight lines and these lines intersect at point O.

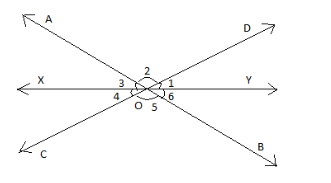
Let us consider that OX is the bisector of \[\angle AOC\] formed by the intersection of AB and CD. Similarly let OY be the bisector of \[\angle BOD\].
As OX is the bisector of \[\angle AOC\], i.e. bisector divides \[\angle AOC\] into two equal angles. So \[\angle 3\] is equal to \[\angle 4.\]
\[\therefore \angle 3=\angle 4......(1)\]
Similarly, OY is the bisector of \[\angle BOD\]. As bisector divides it into two equal angles, \[\angle 1\] will be equal to \[\angle 6.\]
\[\therefore \angle 1=\angle 6......(2)\]
From the figure, we can say that \[\angle 2=\angle 5\], which form the vertically opposite angles.
We know that the sum of all angles formed at a point is \[{{360}^{\circ }}\].
Thus, we can say that, \[\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6={{360}^{\circ }}\]
We know that \[\angle 1=\angle 6;\angle 3=\angle 4;\angle 2=\angle 5\]
\[\begin{align}
  & \therefore \angle 1+\angle 2+\angle 3+\angle 3+\angle 2+\angle 1={{360}^{\circ }} \\
 & 2\angle 1+2\angle 2+2\angle 3={{360}^{\circ }} \\
 & 2\left( \angle 1+\angle 2+\angle 3 \right)={{360}^{\circ }} \\
 & \therefore \angle 1+\angle 2+\angle 3=\dfrac{{{360}^{\circ }}}{2}={{180}^{\circ }} \\
 & \therefore \angle 1+\angle 2+\angle 3={{180}^{\circ }} \\
\end{align}\]
where \[\angle 1=\angle DOY,\angle 2=\angle AOD,\angle 3=\angle AOX.\]
This means that \[\angle DOY+\angle AOD+\angle AOX={{180}^{\circ }}\]
By checking the figure along with the angles, we can make out that
\[\begin{align}
  & \angle XOY=\angle DOY+\angle AOD+\angle AOX \\
 & \therefore \angle XOY={{180}^{\circ }} \\
\end{align}\]
Thus we proved that the bisectors of pairs of vertically opposite angles are on the same straight line.

Note: The last part can also be proved by taking \[\angle 4,\angle 5,\angle 6\].
We found out that
\[\begin{align}
  & \angle 1=\angle 6,\angle 2=\angle 5,\angle 3=\angle 4. \\
 & \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6={{360}^{\circ }} \\
 & 2\left( \angle 4+\angle 5+\angle 6 \right)={{360}^{\circ }} \\
 & \therefore \angle 4+\angle 5+\angle 6={{180}^{\circ }} \\
 & \angle 4=\angle XOC,\angle 5=\angle BOC,\angle 6=\angle BOY \\
 & \angle XOC+\angle BOC+\angle BOY={{180}^{\circ }} \\
 & \angle XOY=\angle XOC+\angle BOC+\angle BOY={{180}^{\circ }} \\
 & \therefore \angle XOY={{180}^{\circ }} \\
\end{align}\]