Question

Prove that the bisector of interior angles of a parallelogram form a rectangle.\[\]

Answer 1

Hint: We take the parallelogram ABDC. We denote the point of intersection of angle bisectors of angles A and B as P, the point of intersection of angle bisectors of angles B and D as , the point of intersection of angle bisectors of angles D and C as R and the point of intersection of angle bisectors of angles C and A as S. The points of intersection form a quadrilateral PQRS. We take the triangle APB and with the fact that sum of the angles $A+P+B={{180}^{\circ }}$ and the sum of co-interior angles $A+B={{180}^{\circ }}$ we prove $P={{90}^{\circ }}$. We similarly take triangles BQD, DRC, CSA to prove $Q=R=S={{90}^{\circ }}$.\[\]

Complete step-by-step answer:
Let us now solve this question.

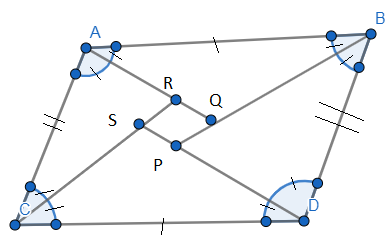
Let us first look at the figure provided below.

Let us observe the triangle APB. We know that the opposite sides of a parallelogram are parallel.
Therefore, AC ll BD and AB is the transversal.
Now, angle A + angle B =${{180}^{\circ }}$ (co – interior angles)
Therefore, we get \[\dfrac{1}{2}A\ +\ \dfrac{1}{2}B\ =\ \dfrac{1}{2}\times 180{}^\circ \ =\ 90{}^\circ \]
Now, in ∆APB, \[\dfrac{1}{2}A\ +\ \dfrac{1}{2}B\ +\ P\ =\ 180{}^\circ \]
\[90^\circ \; + \;P\; = \;180^\circ \left( {\because \dfrac{1}{2}A\; + \;\dfrac{1}{2}B\; = \;90^\circ } \right)\]
$P={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$.Therefore, angle P =${{90}^{\circ }}$
Now, in a similar way, AC ll BD and CD is the transversal.
So, by following the same method as shown above, we get the measure of angle R.
Angle R = ${90}^{\circ}$
Now, as we know that AB ll CD, therefore, the transversal is BD.
Now, angle B + angle D = ${{180}^{\circ }}$ (co – interior angles)
Therefore, we get \[\dfrac{1}{2}B\ +\ \dfrac{1}{2}D\ =\ \dfrac{1}{2}\times 180{}^\circ \ =\ 90{}^\circ \]
Now, in ∆BDQ, \[\dfrac{1}{2}B\ +\ \dfrac{1}{2}D\ +\ Q\ =\ 180{}^\circ \] (angle sum property)
\[90{}^\circ \ +\ Q\ =\ 180{}^\circ \] \[(\because \dfrac{1}{2}B\ +\ \dfrac{1}{2}D\ =\ 90{}^\circ )\]
$Q={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$
Therefore, angle
Now, in a similar way, AB ll CD and AC is the transversal.
So, by following the same method as shown above, we get the measure of angle S.
Angle S = ${{90}^{\circ }}$
So, after solving this question, we get:-
Angle P = angle R = angle Q = angle S = ${{90}^{\circ }}$
And, as all the angles of PQRS have a measure of ${{90}^{\circ }}$, therefore, PQRS is a rectangle.
Hence, proved. \[\]

Note: We note of different angles formed when a transversal cuts two parallel lines. Here are some of them:- Corresponding Angles(equal angles on the same side of the transverse line), Vertically Opposite Angles(equal angles at opposite side at the points of intersection), Linear Pair(supplementary angles at the same side), Alternate Interior Angles(equal angles at different side ), Alternate Exterior Angles(equal angles on both side of the transverse line) Etc.