Question

Prove that the area of trapezium is half of the sum of parallel sides multiplied by the distance between them.

Answer 1

Hint: For proving, this question we will first do construction in the figure of trapezium with proper labelling. Then we will divide trapezium into two triangles with height h. then we will find the area of both the triangles and then we will add the area of triangles to get the area of trapezium.

Complete step-by-step answer:
Before we solve the question, let us see what is trapezium and what the properties of trapezium are.
A trapezium is a 2-D shape and a type of quadrilateral, which has only two parallel sides and the other two sides are non-parallel, where quadrilateral means a polygon or closed shape with four sides and four vertices.
In trapezium, only one pair of opposite sides are parallel and none of sides are equal. A square, rectangle and rhombus are trapezium but trapezium is not a square, rectangle and rhombus.

Now, I question whether we have to prove that the area of trapezium is half of the sum of parallel sides multiplied by the distance between them.
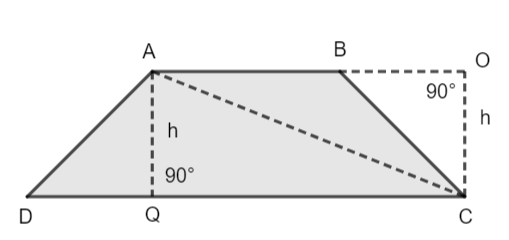
Let, we have a trapezium ABCD, with a pair of parallel sides AB and DC and non – parallel sides AD and BC and height of trapezium is h.
So, we have to prove that Area of Trapezium ABCD $=\dfrac{1}{2}\times h\times (AB+CD)$
Now, firstly we will do some construction. We will firstly construct altitude from vertex A to side DC, and diagonal AC from vertex A to vertex C. Also, we will extend sides AB and a perpendicular line from vertex C meeting extended line AB at point O making angle of ${{90}^{{}^\circ }}$ .
Now from the figure we can see trapezium ABCD is divided into two triangles $\vartriangle ABC$ and $\vartriangle ADC$.
So, area of trapezium = area of triangle $\vartriangle ABC$ + area of triangle $\vartriangle ADC$ ….. ( i )
Now, from the figure we can see, side AQ is equal to OC as both are perpendicular distance equals to height of trapezium h.
Now, we know that area of triangle whose height is h and base is d is equals to $\dfrac{1}{2}\times h\times d$
In figure, for triangle $\vartriangle ABC$, we can see that height of $\vartriangle ABC$ is h and base is AB.
So, area of triangle $\vartriangle ABC$$=\dfrac{1}{2}\times h\times AB$
and, for triangle $\vartriangle ADC$, we can see that height of $\vartriangle ADC$ is h and base is CD.
So, area of triangle $\vartriangle ADC$$=\dfrac{1}{2}\times h\times CD$
Form statement ( i ), we can say that
Area of trapezium ABCD $=\dfrac{1}{2}\times h\times AB+\dfrac{1}{2}\times h\times CD$
Taking, $\dfrac{1}{2}\times h$, common, we get
Area of trapezium ABCD $=\dfrac{1}{2}\times h\times (AB+CD)$
Hence, we proved that the area of trapezium is half of the sum of parallel sides multiplied by the distance between them.

Note: When you do some construction in diagram out of the question, then always mention those construction in the solution and show those construction in diagram. Diagram must be clean and neat. Solve the area of both triangles, individually.