Question

How would you prove that the area of an equilateral triangle constructed on the hypotenuse of the right triangle is equal to the sum of the areas of the equilateral triangle constructed on the legs?

Answer 1

Hint:
According to the question, we need to first construct or draw whatever we want to prove. Constructing makes it easier to prove the given question. Next, we will try to use the Pythagoras theorem and the formula of finding the area of an equilateral triangle.

Complete step by step solution:
Let’s construct a right-angled triangle. The name of the triangle is triangle \[ABC\] in which \[\angle B\] will be the right angle. We will assign \[AB = x\] and \[BC = y\].
Now we need to draw three more triangles. Those three triangles will be equilateral triangles. They will be drawn on the three sides of the right-angled triangle \[ABC\]. We will assume the areas of the \[BC,\,BF,\,AC\]as \[a_1,\,a_2,\,a_3\]respectively.

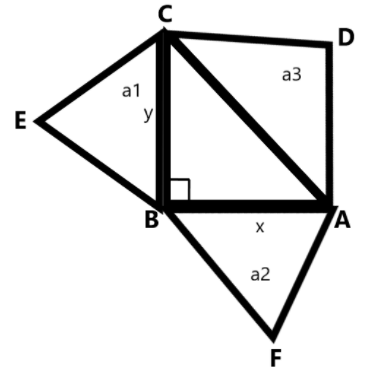
Now, according to the question, we need to prove that:
\[a_3 = a_1 + a_2\]
To prove: \[a_3 = a_1 + a_2\]
Proof:
In the triangle \[ABC\], when we apply Pythagoras theorem, we get:
\[A{C^2} = A{B^2} + B{C^2}\]
Now, when we can also put the value of \[AB = x\]and \[BC = y\]in the equation, and we get:
\[ \Rightarrow A{C^2} = {x^2} + {y^2}\]
When we take off the squares of \[AC\], we get:
\[AC = \sqrt {{x^2} + {y^2}} \]
We know that the area of an equilateral triangle is \[\dfrac{{\sqrt 3 }}{4}{(side)^2}\]
So, the area of the equilateral triangle \[BEC\]which is represented as \[a_1\] is \[\dfrac{{\sqrt 3 }}{4}{(BC)^2}\].
We can also write it as \[\dfrac{{\sqrt 3 }}{4}{(y)^2}\]. So,
\[a_1 = \dfrac{{\sqrt 3 }}{4}{(y)^2}\]
Similarly, the area of the equilateral triangle \[AFB\] which is represented as \[a_2\] is \[\dfrac{{\sqrt 3 }}{4}{(AB)^2}\].
We can also write it as \[\dfrac{{\sqrt 3 }}{4}{(x)^2}\]. So,
\[a_2 = \dfrac{{\sqrt 3 }}{4}{(x)^2}\]
Now, the area of the equilateral triangle \[ACD\] which is represented as \[a_3\]is \[\dfrac{{\sqrt 3 }}{4}{(AC)^2}\].
We can also write it as \[\dfrac{{\sqrt 3 }}{4}{\left( {\sqrt {{x^2} + {y^2}} } \right)^2}\]. When we simplify it, we get:
\[a_3 = \dfrac{{\sqrt 3 }}{4}\left( {{x^2} + {y^2}} \right)\]
Therefore, it is proved that the area of an equilateral triangle constructed on the hypotenuse of the right triangle is equal to the sum of the areas of the equilateral triangle constructed on the legs.

Note:
In Mathematics, Pythagoras theorem is the theorem that says when there is a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the two other sides. The sides are known as perpendicular, base and hypotenuse.