Question

Prove that: $\tan (\pi - x) = - \tan x$ .

Answer 1

Hint:Here in this question we are supposed to use the values and signs of the different trigonometric functions lying in different quadrants. Some trigonometric functions carry positive signs with them in some quadrants and that is all we have to look for to prove the statement.

Complete solution step by step:
Firstly we write down the expression given to us in the question
$\tan (\pi - x) = - \tan x$

For a question like this we simply take the Right Hand Side (RHS) of the equation and by simplifying it reaches to the Left Hand Side (LHS) of the equation.

Taking the LHS of the equation and simplifying it
$\tan (\pi - x)$

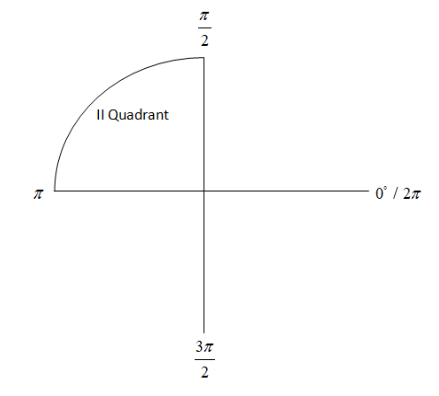
We know that anything which is less than 180 degrees will lie in the 2 nd quadrant of the Cartesian plane which means it lies somewhere here in the arc

As we know that the functions of tangent $(\tan x)$ are positive in 1 st and 3 rd quadrants only

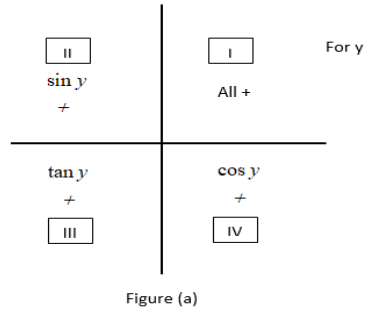
So the expression will be negative after simplifying, although it will not change into cotangent because we are changing it from 180 degrees which means
$\tan (\pi - x) = - \tan x$

Hence, it is proved.

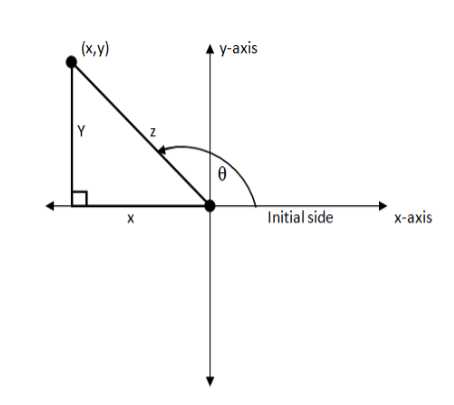
Note: Signs of trigonometric functions are very important to get the right value of the trigonometric ratios. Observing the figure given below we understand that the values of ‘y’ will be positive and since we apply trigonometry to right angle triangles ,it will have a negative base meaning in case of tangent, base will be zero in the 2 nd quadrant i.e.
$\tan \theta = \dfrac{y}{{ - x}} = - \dfrac{y}{x}$

The following figure demonstrates the phenomenon in a better way -