Question

 Prove that $\sin \left( 90{}^\circ -\theta \right)\cos \left( 90{}^\circ -\theta \right)=\dfrac{\tan \theta }{1+{{\tan }^{2}}\theta }$

Answer 1

Hint: In a right triangle, ABC is right-angled at A if $\angle C=\theta $ then $\angle B=90{}^\circ -\theta $. Use the fact that \[\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\] and \[\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}\] and $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$. Hence prove that $\sin \left( 90{}^\circ -\theta \right)=\cos \theta $ and $\cos \left( 90{}^\circ -\theta \right)=\sin \theta $. Finally, divide and multiply by $\cos \theta $ and use the fact that $\dfrac{\sin \theta }{\cos \theta }=\tan \theta $ and ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta $.

Complete step by step answer:
Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine, tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
Observe that sine and cosecant are multiplicative inverses of each other, cosine and secant are multiplicative inverses of each other, and tangent and cotangent are multiplicative inverses of each other.

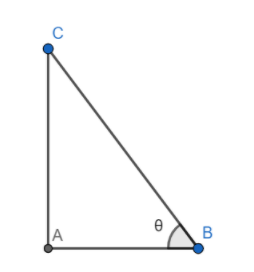
In the given figure ABC is a right-angled triangle right-angled at A
$\angle B=\theta $
Now we know from angle sum property of a triangle, $\angle A+\angle B+\angle C=180$
Substituting the value of $\angle A$ and $\angle B$ we get
\[\begin{align}
  & 90{}^\circ +\theta +\angle C=180{}^\circ \\
 & \Rightarrow \angle C=180{}^\circ -90{}^\circ -\theta \\
 & \Rightarrow \angle C=90{}^\circ -\theta \\
\end{align}\]
Now $\sin C=\dfrac{AB}{BC}$ and $\cos B=\dfrac{AB}{BC}$
Hence, we have
$\sin C=\cos B$
i.e. $\sin \left( 90{}^\circ -\theta \right)=\cos \theta $
Similarly, we can prove that $\cos \left( 90{}^\circ -\theta \right)=\sin \theta $
Also, from Pythagoras theorem, we can prove that ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta $
Now, we have
LHS $=\sin \left( 90{}^\circ -\theta \right)\cos \left( 90{}^\circ -\theta \right)$
Using the above-derived results, we have
LHS $=\cos \theta \sin \theta $
Multiplying and dividing by $\cos \theta $, we get
LHS $={{\cos }^{2}}\theta \dfrac{\sin \theta }{\cos \theta }$
We know that $\dfrac{\sin \theta }{\cos \theta }=\tan \theta $
Hence, we have
LHS $=\dfrac{\tan \theta }{{{\sec }^{2}}\theta }$
We know that ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta $, we get
LHS $=\dfrac{\tan \theta }{1+{{\tan }^{2}}\theta }$

Note: Alternative solution:
We have know that $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$
Hence, we have
$RHS=\dfrac{\sin 2\theta }{2}$
Now, we know that $\sin 2\theta =2\sin \theta \cos \theta $
Using the above identity, we get
$RHS=\dfrac{2\sin \theta \cos \theta }{2}=\sin \theta \cos \theta $
Now, we know that
$\sin \left( 90{}^\circ -\theta \right)=\cos \theta $ and $ \cos \left( 90{}^\circ -\theta \right)=\sin \theta $
Hence, we have
$RHS=\sin \left( 90{}^\circ -\theta \right)\cos \left( 90{}^\circ -\theta \right)$
Hence, we have
RHS = LHS