Question

Prove that ${{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\cos }^{-1}}\left( \dfrac{36}{85} \right)$
${{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\cos }^{-1}}\left( \dfrac{36}{85} \right)$

Answer 1

Hint: We solve this question by first considering the LHS of the given expression and then we use the formula, ${{\sin }^{-1}}x+{{\sin }^{-1}}y={{\sin }^{-1}}\left( x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}} \right)$, if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$. Then we check if our values satisfy the conditions for the formula and then we get the result of sum in inverse of sine. Then we assume obtained value as $\theta $ and find the value of $\cos \theta $ using the formula for Pythagoras theorem $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$ and formulas $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$ and $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$ then find the value of $\theta $ in terms of cosine inverse.

Complete step-by-step solution:
Here we need to prove that ${{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\cos }^{-1}}\left( \dfrac{36}{85} \right)$.
Now let us consider the expression ${{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)$.
Now let us consider the formula, ${{\sin }^{-1}}x+{{\sin }^{-1}}y={{\sin }^{-1}}\left( x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}} \right)$, if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$.
 Now let us check if the values we have to satisfy the given conditions for the above formula.
As we see $\dfrac{8}{17},\dfrac{3}{5}>0$
$\begin{align}
  & \Rightarrow {{\left( \dfrac{8}{17} \right)}^{2}}+{{\left( \dfrac{3}{5} \right)}^{2}} \\
 & \Rightarrow \dfrac{64}{289}+\dfrac{9}{25} \\
 & \Rightarrow \dfrac{1600+2601}{7225} \\
 & \Rightarrow \dfrac{4201}{7225}<1 \\
\end{align}$
So, we can use the above formula. Then by applying above formula we get,
\[\begin{align}
  & {{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right) \\
 & ={{\sin }^{-1}}\left( \dfrac{8}{17}\times \sqrt{1-{{\left( \dfrac{3}{5} \right)}^{2}}}+\dfrac{3}{5}\times \sqrt{1-{{\left( \dfrac{8}{17} \right)}^{2}}} \right) \\
\end{align}\]
Squaring those values inside the square root we get,
\[\begin{align}
  & ={{\sin }^{-1}}\left( \dfrac{8}{17}\times \sqrt{1-\dfrac{9}{25}}+\dfrac{3}{5}\times \sqrt{1-\dfrac{64}{289}} \right) \\
 & ={{\sin }^{-1}}\left( \dfrac{8}{17}\sqrt{\dfrac{25-9}{25}}+\dfrac{3}{5}\sqrt{\dfrac{289-64}{289}} \right) \\
 & ={{\sin }^{-1}}\left( \dfrac{8}{17}\sqrt{\dfrac{16}{25}}+\dfrac{3}{5}\sqrt{\dfrac{225}{289}} \right) \\
\end{align}\]
Taking the square roots for them and simplifying it we get,
\[\begin{align}
  & ={{\sin }^{-1}}\left( \dfrac{8}{17}\times \dfrac{4}{5}+\dfrac{3}{5}\times \dfrac{15}{17} \right) \\
 & ={{\sin }^{-1}}\left( \dfrac{32}{85}+\dfrac{45}{85} \right) \\
 & ={{\sin }^{-1}}\left( \dfrac{77}{85} \right) \\
\end{align}\]
So, we get that,
\[{{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\sin }^{-1}}\left( \dfrac{77}{85} \right)..........\left( 1 \right)\]
Now, let us convert \[{{\sin }^{-1}}\left( \dfrac{77}{85} \right)\] into inverse of cosine as our RHS in the question is in the form of inverse of cosine.
So, let us assume that \[{{\sin }^{-1}}\left( \dfrac{77}{85} \right)=\theta ..........\left( 2 \right)\].
Then we get, $\sin \theta =\dfrac{77}{85}$.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. On comparing that with $\sin \theta =\dfrac{77}{85}$, we get that 77 is the perpendicular and 85 is the hypotenuse.

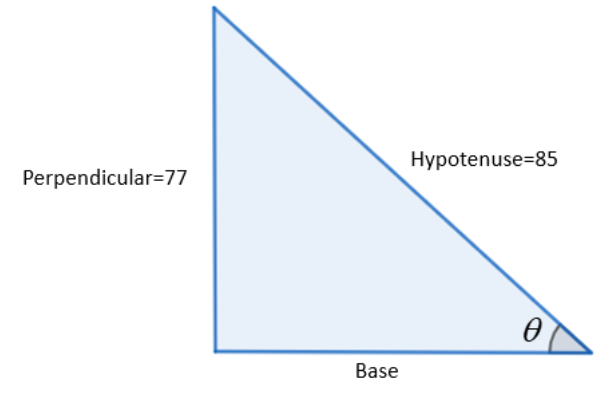
Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{align}
  & \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
 & \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
 & \Rightarrow \text{base}=\sqrt{{{85}^{\text{2}}}-{{77}^{\text{2}}}} \\
 & \Rightarrow \text{base}=\sqrt{7225-5929} \\
 & \Rightarrow \text{base}=\sqrt{1296}=36 \\
\end{align}$
Now, we know that, $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$.
So, we get that $\cos \theta =\dfrac{36}{85}$
Thereby we get, $\theta ={{\cos }^{-1}}\left( \dfrac{36}{85} \right)$.
Substituting in equation (2) we get,
\[{{\sin }^{-1}}\left( \dfrac{77}{85} \right)=\theta ={{\cos }^{-1}}\left( \dfrac{36}{85} \right)\]
Substituting this value in equation (1) we get,
\[{{\sin }^{-1}}\left( \dfrac{8}{17} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\cos }^{-1}}\left( \dfrac{36}{85} \right)\]
Hence Proved.

Note: There is a possibility of one making a mistake while solving this problem by applying the formula for the sum of inverses of sine functions, ${{\sin }^{-1}}x+{{\sin }^{-1}}y={{\sin }^{-1}}\left( x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}} \right)$ without checking the conditions for it, $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}\le 1$. But we need to check if the values we have satisfy these conditions or not and then apply the formula. If they don’t satisfy then we use the formula, ${{\sin }^{-1}}x+{{\sin }^{-1}}y=\pi -{{\sin }^{-1}}\left( x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}} \right)$, if $x,y\ge 0$ and ${{x}^{2}}+{{y}^{2}}>1$.