Question

Prove that ratio of areas of two similar triangles is equal to the square of ratio of their corresponding medians.

Answer 1

Hint: Similar triangles: Those triangles whose size can be changed but shape is same is known as similar triangles.
Median: Line segment from vertex to the opposite which bisects that side is median. Every triangle has 3 medians.

Complete step-by-step answer:
Let us take two triangles $ABC$ and $PQR$ where $AD$ is the median in triangle $ABC$ and
$PM$ is the median in the triangle $PQR$. We have to prove that

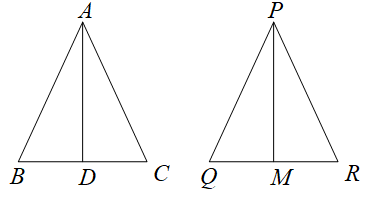
\[\dfrac{{AreaOf\Delta ABC}}{{AreaOf\Delta PQR}} = {\left( {\dfrac{{AD}}{{PM}}} \right)^2}\]
Proof: Since we are given that two triangles $ABC$ & $PQR$ are similar
$\therefore $ $\Delta ABC \sim \Delta PQR$ (given)
$ \Rightarrow $ $\angle B = \angle Q$ (Corresponding angles of similar triangles are also equal)
$ \Rightarrow $$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}}$ (Corresponding scales of similar triangles of same proportion)
$ \Rightarrow $\[\dfrac{{AB}}{{PQ}} = \dfrac{{BD + DC}}{{QM + MR}} = \dfrac{{BD + BD}}{{QM + QM}}\]
$\because $ $AD$ & $PM$ are medians So $BD = DC$ & $QM = MR$
$ \Rightarrow $\[\dfrac{{AB}}{{PQ}} = \dfrac{{2BD}}{{2QM}} = \dfrac{{BD}}{{QM}}\] -------(1)
$\therefore $ In $\Delta ABD$ & $\Delta PQM$
$\angle B = \angle Q$ (already proved)
$\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QM}}$ (From (1)) ----------(2)
$\therefore $ $\Delta ABD \sim \Delta PQM$
$\dfrac{{AB}}{{PQ}} = \dfrac{{DM}}{{PM}}$
Corresponding sides of similar $\Delta $’s in same proportion
\[\dfrac{{AreaOf\Delta ABC}}{{AreaOf\Delta PQR}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\]
\[\dfrac{{AreaOf\Delta ABC}}{{AreaOf\Delta PQR}} = {\left( {\dfrac{{BD}}{{QM}}} \right)^2}\]-----(from equation (2))


Note: 1) From this we can also prove that the ratio of areas of $2$ similar $\Delta $’s is equal to the square of ratio of their altitude.
2) Similarity of triangles can be proved by two methods by taking angles and sides.