Question

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer 1

Hint: Draw a rough diagram of a quadrilateral circumscribing a circle. Join the centre of the circle will all the vertices of the quadrilateral. Consider any one vertex and using S – A – S (side – angle - side) congruence criteria prove that the line joining the vertex with the centre bisects that angle. Finally, use the property of the triangle that, “the sum of all interior angles of a triangle is \[{{180}^{\circ }}\]”, to prove the given statement.

Complete step-by-step answer:
Let us draw a rough diagram of a quadrilateral circumscribing a circle.

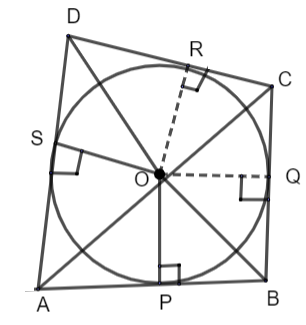
In the above figure we have assumed a quadrilateral ABCD circumscribing a circle with centre O. the circle touches the sides AB, BC, CD and DA of the quadrilateral at P, Q, R and S respectively. So, these sides are behaving like tangents to the circle.
Here, we have joined OP and OS. We know that radius is perpendicular to the tangent at the point of contact. Therefore, OP and OS is perpendicular to AB and DA respectively.
Now, in right angle triangle OPA and OSA, we have,
OP = OS = radius of the circle
OA = OA = common sides
\[\angle OPA=\angle OSA={{90}^{\circ }}\]
Therefore, \[\Delta OPA\] and \[\Delta OSA\] are congruent by S – A – S (side – angle – side) congruence criteria. So, we have,
\[\Rightarrow \angle OAP=\angle OAS\] - (1)
Similarly, we can prove the following three results: -
\[\Rightarrow \angle OBP=\angle OBQ\] - (2)
\[\Rightarrow \angle OCQ=\angle OCR\] - (3)
\[\Rightarrow \angle ODR=\angle ODS\] - (4)
Let us draw the diagram with the following modifications in the assumptions.

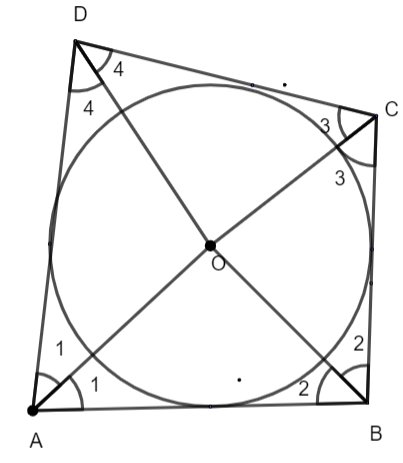
We know that the sum of interior angles of the quadrilateral is \[{{360}^{\circ }}\].
\[\begin{align}
  & \Rightarrow \angle A+\angle B+\angle C+\angle D={{360}^{\circ }} \\
 & \Rightarrow 2\angle 1+2\angle 2+2\angle 3+2\angle D={{360}^{\circ }} \\
 & \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4={{180}^{\circ }} \\
\end{align}\]
Assume the above expression as equation (5).
Now, let us consider triangles AOB and COD. We have to prove that \[\angle AOB+\angle COD={{180}^{\circ }}\]. We know that sum of all the interior angles of a triangle is \[{{180}^{\circ }}\], therefore we have,
\[\Rightarrow \angle 1+\angle 2+\angle AOB={{180}^{\circ }}\] - (6)
And, \[\angle 3+\angle 4+\angle COD={{180}^{\circ }}\] - (7)
Adding equations (6) and (7), we get,
\[\begin{align}
  & \Rightarrow \angle 1+\angle 2+\angle AOB+\angle 3+\angle 4+\angle COD={{360}^{\circ }} \\
 & \Rightarrow \angle AOB+\angle COD={{360}^{\circ }}-\left( \angle 1+\angle 2+\angle 3+\angle 4 \right) \\
\end{align}\]
Using equation (5), we get,
\[\Rightarrow \angle AOB+\angle COD={{360}^{\circ }}-{{180}^{\circ }}={{180}^{\circ }}\]
Hence, we can say that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angle, i.e. \[{{180}^{\circ }}\], at the centre of the circle.
Similarly, we can prove the result for \[\angle BOC\] and \[\angle AOD\].

Note: One may note that supplementary angles means the sum of angles must be \[{{180}^{\circ }}\] and complementary angle means the sum of angles must be \[{{90}^{\circ }}\]. So, do not get confused in these terms. An important thing to note is that the points A, O, C do not lie on a straight line. Here, AO and CO are joined separately so it is not necessary that they are collinear. Similar is the case with points B, O, D.