Question

Prove that “Lines which are parallel to the same line are parallel to each other”.

Answer 1

Hint: First we will draw a diagram for the given question with three lines $l,m,n$and a transversal line t having angles $1,2{\text{ and }}3$. Then first we will prove that line $l||m$ then we will prove that lines $m||n$ and will make two equations for both conditions. Then we will compare both equations and will prove that lines $l||n$.
Complete step-by-step answer:

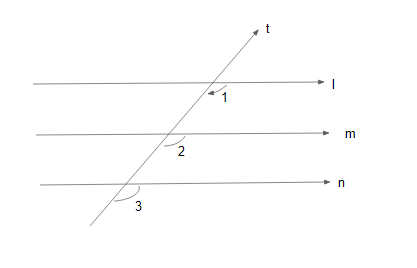
First, we will consider the given diagram:
Here three lines $l,m,n$ are given which are intersecting by the line t.
Given that:
Three lines $l,m,n$ and a transversal line t such that:
$
  l||m \\
  and \\
  m||n \\
 $
We have to prove that: $l||n$
Proof:
For line $l{\text{ and }}m$
With transversal t
$\angle 1 = \angle 2.........\left( 1 \right)$
Because they are corresponding angles.
Now
For line ${\text{m and n}}$
With transversal t
$\angle 2 = \angle 3.........\left( 2 \right)$
Because they are corresponding angles.
Form equation 1 and 2
$\Rightarrow$ $\angle 1 = \angle 3$
They are corresponding angles.
For line $l{\text{ and }}n$ with transversal t, corresponding angles are equal.
Hence lines $l{\text{ and }}n$ are parallel to each other.
Note: First we have to draw the diagram according to the given theorem, in which three lines $l,m,n$, and a transversal line t. We have to remember the concept of corresponding angles because in this question we have to apply the property of corresponding angles to prove lines $l{\text{ and }}n$ are parallel to each other.