Question

Prove that in a parallelogram, the bisector of any two consecutive angles intersect at the right angle.

Answer 1

Hint: Parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and also opposite angles of a parallelogram are equal. One of the properties of a parallelogram says that the sum of any two consecutive angles is 180; hence in this question, find the value of the two consecutive angles and then find their bisecting angles.
In this question, we need to prove that the bisector of any two consecutive angles intersect at the right angle for which we need to follow the above discussed property of the parallelogram.

Complete step by step answer:
 In the given figure
Side AD is parallel to BC, and AB is parallel to DC where the side BC is transversal, hence
\[
  AD\parallel BC \\
  AB\parallel DC \\
 \]

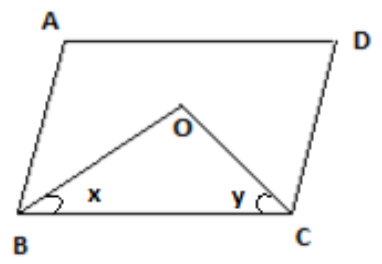
Since one of the properties of parallelogram say the sum of the consecutive angle of a parallelogram is a supplementary angle hence, we can write,
\[\angle ABC + \angle DCB = {180^ \circ }\]
Now draw a line OB bisecting \[\angle B\]and a line OC bisecting \[\angle C\]joining at O since line OB and OC bisects the angle; hence we can say
\[\angle OBC = \dfrac{{\angle ABC}}{2}\]
\[\angle OCB = \dfrac{{\angle DCB}}{2}\]
Hence in the \[\vartriangle OBC\]
\[
  \angle OBC + \angle OCB + \angle BOC = 180 \\
  x + y + \angle BOC = 180 \\
 \]
This can be written as
\[\dfrac{{\angle ABC}}{2} + \dfrac{{\angle DCB}}{2} + \angle BOC = 180\]
Hence by solving
\[\dfrac{1}{2}\left( {\angle ABC + \angle DCB} \right) + \angle BOC = 180\]
Since\[\angle ABC + \angle DCB = {180^ \circ }\]hence we can write

\[
  \dfrac{1}{2}\left( {\angle ABC + \angle DCB} \right) + \angle BOC = 180 \\
  \dfrac{1}{2} \times 180 + \angle BOC = 180 \\
  90 + \angle BOC = 180 \\
  \angle BOC = {90^ \circ } \\
 \]
So the value of\[\angle BOC = {90^ \circ }\],
Therefore we can say the bisector of any two consecutive angles intersect at the right angle.
Hence proved.

Note: A property of that parallelogram says that if a parallelogram has all sides equal, then their diagonal bisector intersects perpendicularly. An angle bisector is a ray that splits an angle into two consecutive congruent, smaller angles.