Question

Prove that if these parallel lines are intersected by a transversal, then prove that the bisectors of the interior angle form a rectangle.

Answer 1

Hint: Make a rough diagram that shows the situation given in the question. Then use the properties of parallel lines and transversal lines to prove that opposite sides are parallel (of the rectangle) and that the interior angles are right angles.

Complete step by step solution:
Consider: AB and CD are 2 parallel lines selected by a transversal L. X and Y are the point of intersection of L with AB and CD respectively. ХP,XQ,YP and YQ are the angle bisectors of angles $\angle AXY,\angle BXY,\angle CYX$ and $\angle DYX$

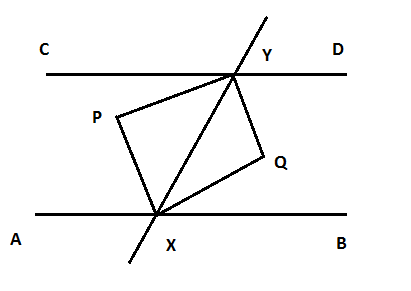
To prove:
The figure obtained on going YP, YQ, XP, XQ is a rectangle or PXQY is a rectangle.
Proof:
As $AB\parallel CD$ and line L is a transversal.
$\therefore \angle AXY=\angle DYX$ (pair of alternate angle)
$\Rightarrow \dfrac{1}{2}\angle AXY=\dfrac{1}{2}\angle DYX$
$\Rightarrow {{\theta }_{1}}={{\theta }_{4}}$ as $\left( {{\theta }_{1}}=\dfrac{1}{2}\angle AXY\text{ and }{{\theta }_{4}}=\dfrac{1}{2}\angle DYX \right)$
This implies that$PX\parallel YQ$. …….. 1
($\because $ if a transversal intersects two lines in such a way that a pair of alternate interior angles are equal, then two lines are parallel.)
Now, $\angle BXY=\angle CYX$ (pair of interior angle)
$\Rightarrow \dfrac{1}{2}\angle BXY=\dfrac{1}{2}\angle CYX$
$\Rightarrow {{\theta }_{2}}={{\theta }_{3}}$ as $\left( {{\theta }_{2}}=\dfrac{1}{2}\angle BXY\text{ and }{{\theta }_{3}}=\dfrac{1}{2}\angle CYX \right)$
This further implies that PY is parallel to XQ ….. 2
(if a transversal intersects two lines in such a way that a pair of internal angles alternate to each other are equal, then two lines are parallel).
From 1 and 2 we get,
PYXQ is a parallelogram
(as the opposite sides are parallel to each other)
$\angle CYD=180{}^\circ $
$\dfrac{1}{2}\angle CYD=90{}^\circ $
$\Rightarrow \dfrac{1}{2}\left( \angle CYX+\angle DYX \right)=90{}^\circ $
$\Rightarrow {{\theta }_{3}}+{{\theta }_{4}}=90{}^\circ $
$\Rightarrow \angle PYQ=90{}^\circ $
Also,${{\theta }_{3}}={{\theta }_{1}}$
${{\theta }_{4}}={{\theta }_{2}}$
$\Rightarrow {{\theta }_{3}}+{{\theta }_{4}}={{\theta }_{1}}+{{\theta }_{2}}=90{}^\circ $.
Hence, PYQX is a rectangle.
Hence proved.

Note: Alternate angles are the two angles formed when the line crosses two other lines that lie on the Opposite sides of the transversal line and on opposite relative sides of the other lines.