Question

Prove that if the sum of two adjacent angles is ${{180}^{{}^\circ }}$, then the non-common arms are two opposite rays.

Answer 1

Hint: We will assume these two rays CA and CB are not opposite to each other, and then we will draw a ray CE which is opposite to CA such that ACE is a straight line. We will try to show that $\angle ACB$ is exactly the same as $\angle ACE$ which contradicts our assumption and then the given condition will be fulfilled.

Complete step-by-step answer:
It is given in the question that the sum of two adjacent angles is ${{180}^{{}^\circ }}$ then we have to prove that their non-common arms are two opposite rays.
Basically rays means, straight line having no end point. To show that two non-common arms are opposite to each other, we will first assume that they are not opposite to each other.

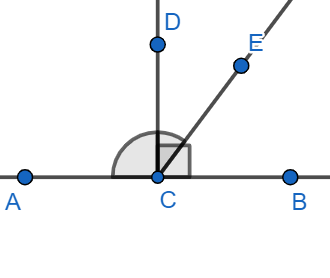
According to the question, we have $\angle ACD+\angle BCD={{180}^{{}^\circ }}....(i)$
Also, we have assumed that CA is not opposite to CB. We have assumed that CE is opposite to CA also sum of $\angle ACD\text{ }and\text{ }\angle ECD$ is equal to ${{180}^{{}^\circ }}$, we get-
$\angle ACD+\angle ECD={{180}^{{}^\circ }}......(ii)$
On subtracting equation 1 and equation 2, we get,
$\left( \angle ACD+\angle BCD \right)-\left( \angle ACD+\angle ECD \right)={{180}^{{}^\circ }}-{{180}^{{}^\circ }}$ solving further, we get
$\angle BCD-\angle ECD=0$ therefore,
$\angle BCD=\angle ECD....(iii)$
But we know that CB and CE on the same side of CD, therefore, equation 3 is only possible if CE and CB coincide, and we know that CE is opposite to CA, thus CB is also opposite to CA.
Hence proved.

Note: Students may confuse in the last step that CE and CB are two different rays. So, how can we say that they coincide, and they may skip this part of the question to solve in the examination. But it is very clear that if we do not assume that CE and CB coincide then we will not be able to show that ray CA is opposite to ray CB.