Question

Prove that if in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.

Answer 1

Hint: In this question, we have been asked to prove that if the two pairs of opposite angles of a quadrilateral are equal, then it is a parallelogram. Find the sum of the angles of the quadrilateral. Using this sum and property that if the angles on the same side of the transversal are supplementary, then the two lines are parallel, prove both the pair of sides to be parallel. Once proven parallel, you can tell that the quadrilateral is a parallelogram.

Complete step-by-step solution:
We have been asked to prove that if the two pairs of opposite angles of a quadrilateral are equal, then it is a parallelogram. We will start by writing what is given and is to be proved.

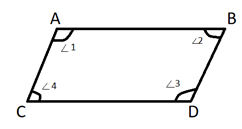
It is given that:
1) a quadrilateral ABCD.
2) pair of equal opposite angles.
$ \Rightarrow \angle 1 = \angle 3,\angle 2 = \angle 4$
To prove: Quadrilateral ABCD is a parallelogram.
Proof: At first, we will find the sum of the angles.
We know that the angle sum property of a quadrilateral says that the sum of all the angles is $360^\circ $.
Therefore, $\angle 1 + \angle 2 + \angle 3 + \angle 4 = 360^\circ $
We also know that $\angle 1 = \angle 3,\angle 2 = \angle 4$. Putting in above equation,
$ \Rightarrow \angle 1 + \angle 2 + \angle 1 + \angle 2 = 360^\circ $
Grouping together,
$ \Rightarrow 2\left( {\angle 1 + \angle 2} \right) = 360^\circ $
$ \Rightarrow \angle 1 + \angle 2 = 180^\circ $ …. (1)
Also, we know that $\angle 2 = \angle 4$.
Therefore $\angle 1 + \angle 4 = 180^\circ $…. (2)
Case 1: Consider lines $AC$ and $BD$. $AB$ is the transversal of $AC$ and $BD$.
$\angle 1$ and $\angle 2$ are two angles on the same side of the transversal $AB$.
According to a property, if the angles on the same side of the transversal are supplementary, then the two lines are parallel.
We know from equation (1) that $\angle 1 + \angle 2 = 180^\circ $.
Therefore, the lines $AC$ and $BD$ are parallel to each other.
Case 2: Consider lines $AB$ and $CD$. $AC$ is the transversal of $AB$ and $CD$.
$\angle 1$ and $\angle 4$ are two angles on the same side of the transversal $AC$.
According to a property, if the angles on the same side of the transversal are supplementary, then the two lines are parallel.
We know from equation (2) that $\angle 1 + \angle 4 = 180^\circ $.
$\therefore $ The lines $AB$ and $CD$ are parallel to each other.

Now, since both the pairs of opposite sides are parallel, ABCD is a parallelogram.

Note: We must know that a quadrilateral can be defined as a closed, two-dimensional shape which has four straight sides. The polygon has four vertices or corners. We can find the shape of quadrilaterals in various things around us, like in a chess board, a deck of cards, a kite, and a tub of popcorn, a sign board and in an arrow.
We have to mind that a quadrilateral is a plane figure made with four line segments closing in a space.